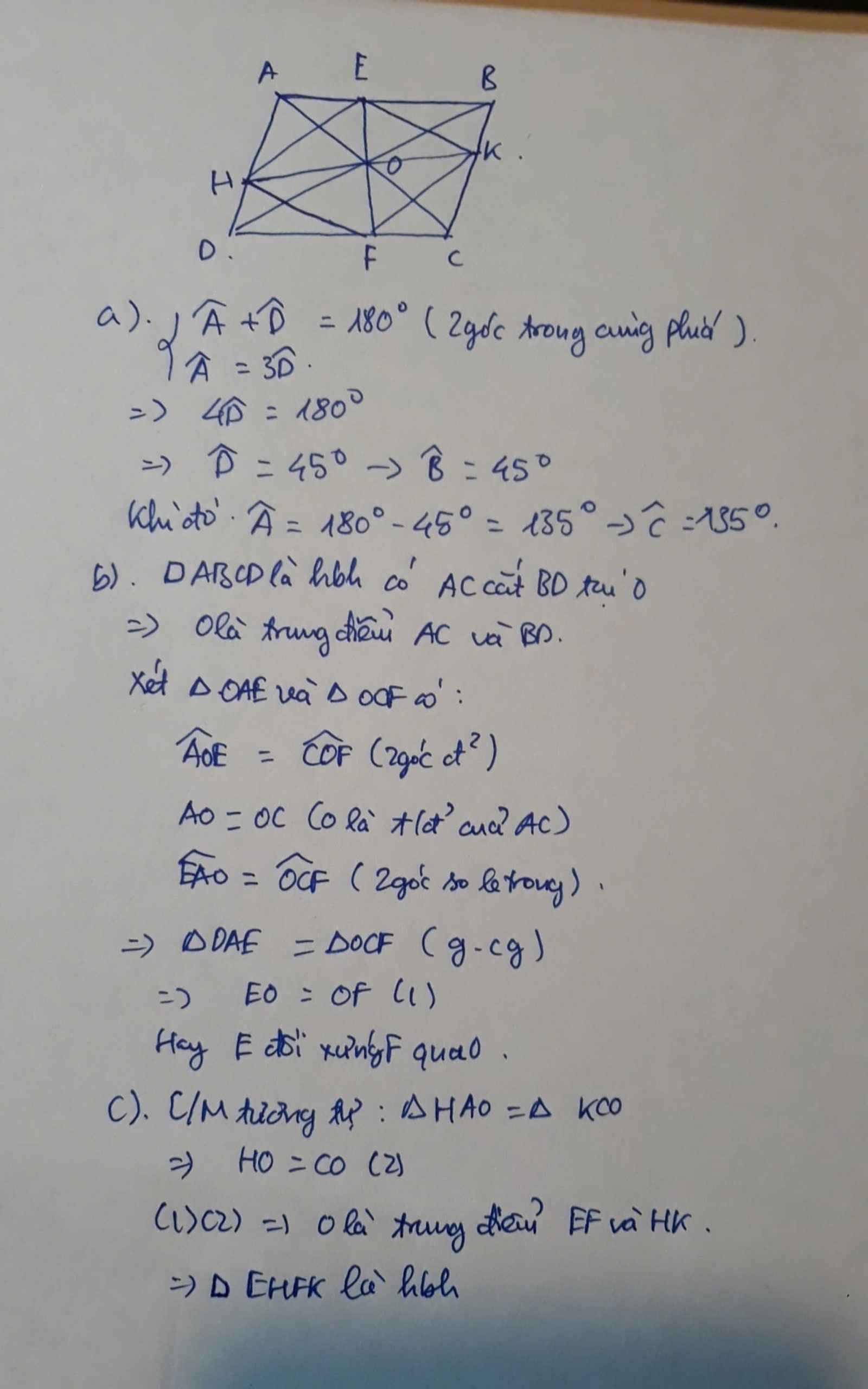Question

Cho hình bình hành ABCD có góc A= 3D

1) tính các góc hình bình hành ABCD

2) gọi O là giao điểm AC và BD. Qua O vẽ đường thẳng x cát AB, CD tại E;F. Qua O vẽ đường thẳng y cắt AD, CB tại H;K. Chứng tỏ E và F đối xứng qua O

3) tứ giác EKFH là hình gì? vì sao?

vẽ hình giúp e lun ạaaa

 

Answer 1

Answer 2

*hình dưới bình luận*
a, Vì ABCD là hình bình hành ⇒ AB // CD
                                            \(\Rightarrow\widehat{BAD}+\widehat{ADC}=180^o\) (2 go'c trong cùng phía)
                                            \(\Rightarrow3\widehat{ADC}+\widehat{ADC}=180^o\) (do \(\widehat{3ADC}=\widehat{BAD}\))
                                            \(\Rightarrow\widehat{ADC}=180^o:4=45^o\); \(\widehat{BAD}=180^o-45^o=135^o\)
Vì ABCD là hình bình hành \(\Rightarrow\widehat{BAD}=\widehat{BCD}=135^o;\widehat{ADC}=\widehat{ABC}=45^o\) (t/chat hinh binh hanh)
b, Vì O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.
⇒ O là trung điểm của AC, BD⇒ OA=OD=OB=OC (t/c hình bình hành)
Xét △ OAE, △OCF có:
\(\widehat{EOA}=\widehat{FOC}\) (2 góc đối đỉnh)
\(OA=OC\)
\(\widehat{EAO}=\widehat{FCO}\) (AB// CD)
⇒ △OAE = △OCF (g-c-g) ⇒ OE = OF ⇒ E và F đối xứng nhau qua O (đpcm)
c, Chứng minh tương tự như câu b ta có K và H đối xứng nhau qua O
Xét tứ giác EKFH có: EK và EH cắt nhau tại O, O là trung điểm của EK và FH
⇒ tứ giác EKFH là hình bình hành (đpcm)