Các câu hỏi tương tự
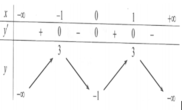
Cho hàm số yf(x) xác định, liên tục trên
ℝ
và có bảng biến thiên như hình sau: Đồ thị hàm số cắt đường thẳng y -2018 tại bao nhiêu điểm ? A. 4 B. 0 C. 2 D. 1
Đọc tiếp
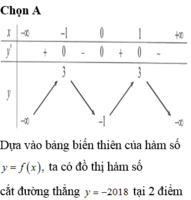
Cho hàm số y=f(x) xác định, liên tục trên ℝ và có bảng biến thiên như hình sau:
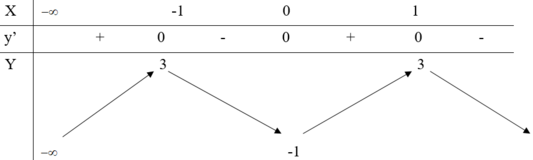
Đồ thị hàm số cắt đường thẳng y = -2018 tại bao nhiêu điểm ?
A. 4
B. 0
C. 2
D. 1
Cho hàm số y f(x) xác định và có đạo hàm trên
R
±
1
. Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số y f(x) có tất cả bao nhiêu đường tiệm cận? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y = f(x) xác định và có đạo hàm trên R \ ± 1 . Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số y = f(x) có tất cả bao nhiêu đường tiệm cận?
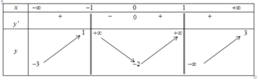
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số yf(x) xác định trên
ℝ
1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽHàm số
y
f
(
x
)
có bao nhiêu điểm cực trị? A. 4. B. 3. C. 2. D. 5.
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ \ 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ
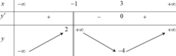
Hàm số y = f ( x ) có bao nhiêu điểm cực trị?
A. 4.
B. 3.
C. 2.
D. 5.
Cho hàm số yf(x) xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Hỏi điểm cực tiểu của đồ thị hàm số y f(x) là điểm nào ? A. x-2 B. y-2 C. D.
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R và có đồ thị là đường cong trong hình vẽ bên.
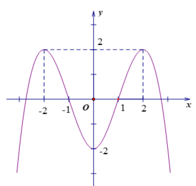
Hỏi điểm cực tiểu của đồ thị hàm số y= f(x) là điểm nào ?
A. x=-2
B. y=-2
C. ![]()
D. ![]()
Cho hàm số f(x) xác định trên R và có đồ thị của hàm số y= f’(x) như hình vẽ bên.

Hàm số y= f( x+ 2018) có mấy điểm cực trị?
A. 1
B. 2
C. 3
D. 4
Cho hàm số yf(x) xác định và liên tục trên
ℝ
. Đồ thị của hàm số f(x) như hình bên. Số điểm cực trị của đồ thị hàm số yf(f(x)) bằng? A. 8. B. 9 C. 10. D. 11.
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên ℝ . Đồ thị của hàm số f(x) như hình bên. Số điểm cực trị của đồ thị hàm số y=f(f(x)) bằng?
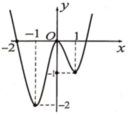
A. 8.
B. 9
C. 10.
D. 11.
Cho hàm số f(x) có đạo hàm f(x) xác định, liên tục trên
ℝ
và có đồ thị f(x) như hình vẽ bên. Hàm số y f(x) đồng biến trên khoảng nào dưới đây?
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

![]()
![]()
![]()
![]()
Cho hàm số y f( x) có đạo hàm f’(x) xác định, liên tục trên R và f’( x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng? A. Hàm số đồng biến trên ( 1; + ∞) B. Hàm số đồng biến trên (-∞;-1) và (3; + ∞) C. Hàm số nghịch biến trên (- ∞; -1) D. Hàm số đồng biến trên
Đọc tiếp
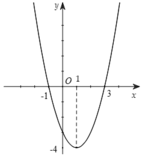
Cho hàm số y= f( x) có đạo hàm f’(x) xác định, liên tục trên R và f’( x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên ( 1; + ∞)
B. Hàm số đồng biến trên (-∞;-1) và (3; + ∞)
C. Hàm số nghịch biến trên (- ∞; -1)
D. Hàm số đồng biến trên ![]()
Cho hàm số
y
f
(
x
)
xác định, liên tục trên đoạn [−2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số
y
f
(
x
)
đạt cực đại tại điểm nào dưới đây? A. x-2 B. x-1 C. x1 D. x2
Đọc tiếp
Cho hàm số y = f ( x ) xác định, liên tục trên đoạn [−2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số y = f ( x ) đạt cực đại tại điểm nào dưới đây?
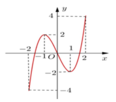
A. x=-2
B. x=-1
C. x=1
D. x=2