\(f'\left(x\right)=0\Rightarrow x=0;82\)
\(u=x^4-18x^2+m\)
\(u'=4x^3-36x=0\Rightarrow x=\left\{-3;0;3\right\}\)
BBT hàm u:
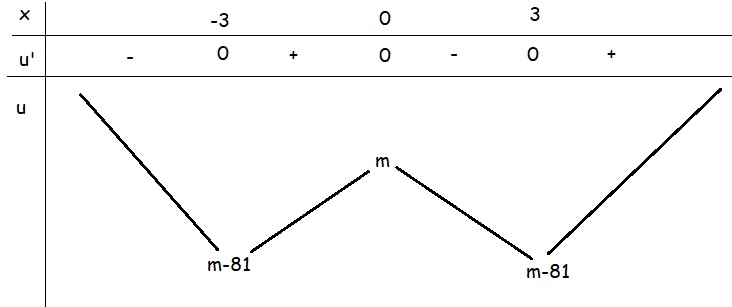
Do u có 3 cực trị nên hàm có đúng 7 cực trị khi 2 đường thẳng \(y=0\) và \(y=82\) cắt \(u\left(x\right)\) tại tổng cộng 4 điểm nghiệm đơn
TH1: \(y=0\) ko cắt (hoặc chỉ tiếp xúc) u(x), còn \(y=82\) cắt u(x) tại 4 điểm pb
\(\Rightarrow\left\{{}\begin{matrix}m-81\ge0\\m-81< 82< m\end{matrix}\right.\) \(\Leftrightarrow82< m< 163\)
Có 80 m nguyên dương
TH2: y=0 và y=82 đều cắt u(x) tại 2 điểm pb
\(\Rightarrow\left\{{}\begin{matrix}m\le0\\m\le82\end{matrix}\right.\) \(\Rightarrow m\le0\) (ko có m nguyên dương)
C đúng
Đúng 0
Bình luận (0)



