Ta có: 2 f x - 3 = 0
⇔ f x = 3 2
⇒ Số nghiệm của phương trình 2 f x - 3 = 0
là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = 3 2
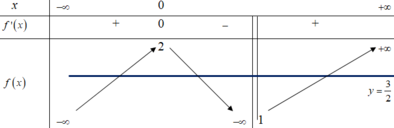
Dựa vào BBT ta thấy đường thẳng y = 3 2 cắt đồ thị hàm số tại 3 điểm phân biệt.
Chọn A.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số y f (x) có bảng biến thiên như sau Số nghiệm thực của phương trình 2 f (x) + 3 0 là A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên như sau
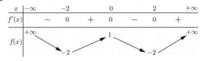
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số y=f(x) có bảng biến thiên như sau:
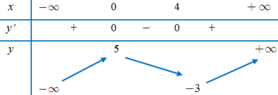
Số nghiệm của phương trình f(x)-3=0 là
A. 3
B. 0
C. 2
D. 1
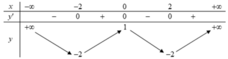
Cho hàm số y f(x) có bảng biến thiên như sau: Số nghiệm thực của phương trình 2f(x) + 3 0 là A. 4. B. 3. C. 2. D. 1.
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2f(x) + 3 = 0 là
A. 4.
B. 3.
C. 2.
D. 1.
Cho hàm số y f(x) có bảng biến thiên như sau Số nghiệm thực của phương trình
f
(
4
x
-
x
2
)
-
2
0
là A. 4 B. 0 C. 2 D. 6
Đọc tiếp
Cho hàm số y= f(x) có bảng biến thiên như sau
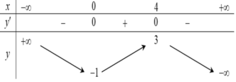
Số nghiệm thực của phương trình f ( 4 x - x 2 ) - 2 = 0 là
A. 4
B. 0
C. 2
D. 6
Cho hàm số yf(x) liên tục trên R có bảng biến thiên như sau: Số nghiệm của phương trình f(x)-20 là: A. 4. B. 0. C. 2. D. 3.
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có bảng biến thiên như sau:
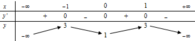
Số nghiệm của phương trình f(x)-2=0 là:
A. 4.
B. 0.
C. 2.
D. 3.
Cho hàm số y=f(x) có bảng biến thiên như sau
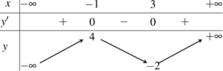
Số nghiệm phương trình 2f(x) -3 = 0 là:
A. 2
B. 0
C. 1
D. 3
Cho hàm số y f (x) có bảng biến thiên như sau: Số nghiệm của phương trình f(x) – x2 + 2x - 1 0 là
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên như sau: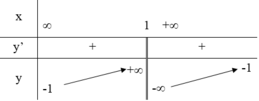
Số nghiệm của phương trình f(x) – x2 + 2x - 1 = 0 là
Cho hàm số f(x) có bảng biến thiên như sau:
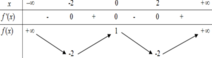
Số nghiệm thực của phương trình f(f(x)) + 2 = 0 là
A. 4
B. 3
C. 2
D. 6
Cho hàm số y f(x) có bảng biến thiên như sau Số nghiệm của phương trình f(x) - 4 0 là A. 2 B. 3 C. 0 D. 1
Đọc tiếp
Cho hàm số y =f(x) có bảng biến thiên như sau
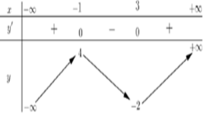
Số nghiệm của phương trình f(x) - 4 =0 là
A. 2
B. 3
C. 0
D. 1
Cho hàm số y = f(x) có bảng biến thiên như sau:
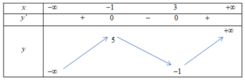
Số nghiệm phương trình f(|x - 1|) - 5 = 0 là ?
A. 8
B. 6
C. 4
D. 2