Chọn D
Ta có:
y ' = − sin 2 π 3 + 2 x . 2 π 3 + 2 x ' = − 2. sin 2 π 3 + 2 x
Theo giả thiết Ta có: y ' = 0 ⇔ sin 2 π 3 + 2 x = 0
⇔ 2 π 3 + 2 x = k π ⇔ x = − π 3 + k π 2 k ∈ ℤ
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
f
(
x
)
1
+
cos
x
(
x
-...
Đọc tiếp
f ( x ) = 1 + cos x ( x - π ) 2 , k h i x ≠ π m , k h i x = π Tìm m để f (x) liên tục tại x = π
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
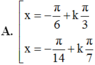
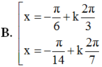
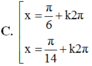
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
Cho hàm số f(x) = sin3x.
Tính f''(-π/2), f''(0), f''(π/18)
Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = 2 sin(2x + π 4 ) (*)
A: 1
B: 2
C: 3
D: 4
Tổng các nghiệm của phương trình:
sin
2
(
2
x
-
π
/
4
)
-
3
cos
(
3
π
/
4
-
2
x
)
+
2
0
(
1
)
trong khoảng (0;2π) là: A. 7π/8 B. 3π/8 C. π D. 7π/4
Đọc tiếp
Tổng các nghiệm của phương trình: sin 2 ( 2 x - π / 4 ) - 3 cos ( 3 π / 4 - 2 x ) + 2 = 0 ( 1 ) trong khoảng (0;2π) là:
A. 7π/8
B. 3π/8
C. π
D. 7π/4