Cho hàm số \(f\left(x\right)=x+\dfrac{1}{x-1}\) với x > 1.
a) Tính \(\lim\limits_{x\rightarrow1^+}f\left(x\right),\lim\limits_{x\rightarrow+\infty}f\left(x\right).\)
b) Lập bảng biến thiên của hàm số f(x) trên khoảng (1; + \(\infty\)).
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số f(x) trên khoảng (1; +\(\infty\)).
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:
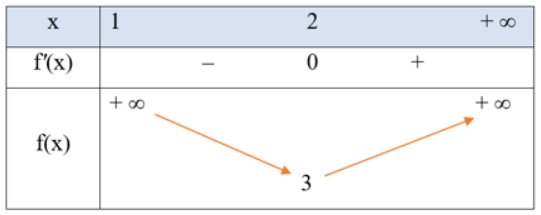
c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.


