Đáp án B.
I = ∫ − 2 5 f x d x − 4 ∫ − 2 5 g x d x − ∫ − 2 5 d x = ∫ − 2 5 f x d x + 4 ∫ 5 − 2 g x d x − x − 2 5 = 8 + 4.3 − 5 + 2 = 13.
Đáp án B.
I = ∫ − 2 5 f x d x − 4 ∫ − 2 5 g x d x − ∫ − 2 5 d x = ∫ − 2 5 f x d x + 4 ∫ 5 − 2 g x d x − x − 2 5 = 8 + 4.3 − 5 + 2 = 13.
Cho hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số y=f(x) , y=g(x) và hai đường thẳng x= a, x= b(a < b) Diện tích của D được tính theo công thức
A. S = ∫ a b f x - g x d x
B. S = ∫ a b f x - g x d x
C. ∫ a b f x d x - ∫ a b g x d x
D. S = ∫ b a f x - g x d x
Cho hàm số y=f(x) liên tục và dương trên R , hình phẳng giới hạn bởi các đường y = g ( x ) = ( x - 1 ) . f ( x 2 - 2 x + 1 ) , trục hoành, x=1,x=2 có diện tích bằng 5. Tính tích phân I = ∫ 0 1 f ( x ) dx .
A. I = 10.
B. I = 20.
C. I = 5.
D. I = 9
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Cho hàm số y = f ( x ) , y = g ( x ) liên tục trên đoạn [ a ; b ] ( a < b ) . Hình phẳng D giới hạn bởi đồ thị hai hàm số y = f ( x ) , y = g ( x ) và hai đường thẳng x = a, x= b có diện tích là
A. S D = ∫ a b f ( x ) − g ( x ) d x .
B. S D = ∫ a b f ( x ) − g ( x ) d x .
C. S D = π ∫ a b f ( x ) − g ( x ) d x .
D. S D = ∫ b a f ( x ) − g ( x ) d x .
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [ a; b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a , x = b a < b . Diện tích S của hình phẳng D được tính theo công thức
A. S = ∫ a b f x − g x d x
B. S = ∫ a b g x − f x d x
C. S = ∫ a b f x − g x d x
D. S = ∫ a b f x − g x d x
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn: ∫ 1 3 [ f ( x ) + 3 g ( x ) ] d x = 10 và ∫ 1 3 [ 2 f ( x ) - g ( x ) ] d x = 6 . Tính I = ∫ 1 3 [ f ( x ) + g ( x ) ] d x
A. I=8
B. I=9
C. I=6
D. I=7
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
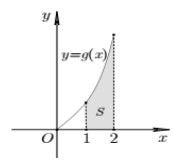
Cho hàm số y=f(x) liên tục trên R và hàm số y = g ( x ) = x f ( x 2 ) có đồ thị trên đoạn [0; 2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2, tính tích phân I = ∫ 1 4 f ( x ) d x
A. 5/4
B. 5/2
C. 5
D. 10
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x