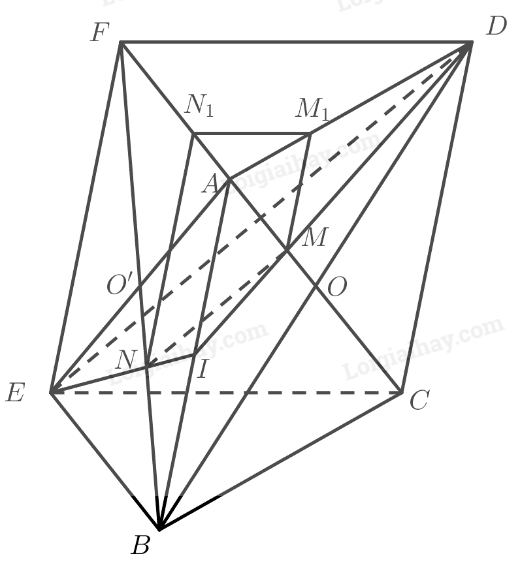
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng khác nhau. Lấy các điểm \(M,N\) lần lượt thuộc các đường chéo \(AC\) và \(BF\) sao cho \(MC = 2MA;NF = 2NB\). Qua \(M,N\) kẻ các đường thẳng song song với \(AB\), cắt các cạnh \(AD,AF\) lần lượt tại \({M_1},{N_1}\). Chứng minh rằng:
a) \(MN\parallel DE\);
b) \({M_1}{N_1}\parallel \left( {DEF} \right)\);
c) \(\left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\).
\(\begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{BN}}{{BF}} = \frac{1}{3}\\M{M_1}\parallel AB \Rightarrow \frac{{A{M_1}}}{{A{\rm{D}}}} = \frac{{IM}}{{I{\rm{D}}}} = \frac{1}{3}\end{array} \right\} \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{A{M_1}}}{{A{\rm{D}}}}\\\left. \begin{array}{l} \Rightarrow {M_1}{N_1}\parallel DF\\DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow {M_1}{N_1}\parallel \left( {DEF} \right)\end{array}\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB\parallel EF\\EF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow N{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1},N{N_1} \subset \left( {MN{N_1}{M_1}} \right)\end{array} \right\} \Rightarrow \left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\)



