a, Chú ý: C M A ^ = D N A ^ = 90 0
b, Vẽ OP ⊥ MA; O'Q ⊥ NA
Chú ý hình thang vuông OPQO’ có EA là đường trung bình

a, Chú ý: C M A ^ = D N A ^ = 90 0
b, Vẽ OP ⊥ MA; O'Q ⊥ NA
Chú ý hình thang vuông OPQO’ có EA là đường trung bình
Qua A ở ngoài đường tròn ( O ; R ) vẽ cát tuyến ABC với đường tròn . Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K . Qua K kẻ đường thẳng vuông với AO cắt AO tại H và cắt đường tròn ( O ) tại E và F ( E nằm giữa K và F ). Gọi M là giao điểm của Ok và BC . Chứng minh :
a) Tứ giác EMOF nội tiếp .
b) AE và AF là các tiếp tuyến của đường tròn ( O ).
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm (O). Từ B và C vẽ hai tiếp tuyến của đường tròn, hai tiếp tuyến này cắt nhau ở D. Qua D vẽ một cát tuyến sonng song với AB, cát tuyến này cắt đường tròn tại các điểm M và N và cắt cạnh AC tai I
a) Chứng minh tứ giác OBDC nội tiếp đường tròn (O)
b) Chứng minh I là trung điểm của dây MN
Qua A ở ngoài đường tròn ( O ; R ) vẽ cát tuyến ABC với đường tròn . Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K . Qua K kẻ đường thẳng vuông với AO cắt AO tại H và cắt đường tròn ( O ) tại E và F ( E nằm giữa K và F ). Gọi M là giao điểm của OK và BC biết tứ giác EMOF nội tiếp . Chứng minh : AE và AF là các tiếp tuyến của đường tròn ( O ).
Cho đường tròn (O ; R), đường kính AB. M là một điểm nằm giữa O và B. Đường thẳng kẻ qua trung điểm E của AM vuông góc với AB cắt đường tròn (O) ở C và D.
a) Tứ giác ACMD là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt tia OA ở I. Chứng minh ID là tiếp tuyến của đường tròn (O).
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC. Chứng minh:
a) Tứ giác EMOF nội tiế.
b) AE, AF là tiếp tuyến của đường tròn.
Cho đường tròn (O). Từ điểm M nằm ngoài đường tròn (O) hẻ hai tiếp tuyến MA,MB của (O) ( với A,B là các tiếp điểm). Kẻ AH vuông góc với MB tại H. Đường thẳng AH cắt (O) tại N ( khác A). Đường tròn đường kính NA cắt các đường thẳng AB và MA theo thứ tự tại I và K. a) Chứng minh tứ giác NHBI nội tiếp. b) Chứng minh tam giác NHI đồng dạng với tam giác NIK. c) Gọi C là giao điểm của NB và HI, gọi D là giao điểm của Na và KI, Đường thẳng CD cắt MA tại E. Chứng minh CI = EA.
Cho đường tròn (O) điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF).Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO)
a, Chứng minh MA. MB = ME.MF
b, Gọi H là hình chiêu vuông góc của điểm c lên đuờng thẳng MO. Chứng minh tứ giác AHOB nội tiếp
c, Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K. Gọi S là giao điểm của hai đường thẳng CO và KF. Chứng minh các đường thẳng MS và KC vuông góc nhau
d, Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp các tam giác EFS và ABS và T là trung điểm của KS. Chứng minh ba điểm P, Q, T thẳng hàng
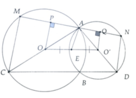
Cho hai đường tròn tâm O và O’ tiếp xúc ngoài tại A. Qua A kẻ một cát tuyến cắt (O) ở B và cắt (O') ở C. Kẻ các đường kính BOD và CO'E của hai đường tròn trên
a, Chứng minh BD song song CE
b, Chứng minh ba điểm D, A, E thẳng hàng
c, Nếu (O) bằng (O') thì tứ giác BDCE là hình gì? Tại sao?