Chọn D.
Gọi u 1 → ; u 2 → lần lượt là vectơ chỉ phương của đường thẳng d1; d2.
Áp dụng công thức ta có cosin góc giữa hai đường thẳng là:

Chọn D.
Gọi u 1 → ; u 2 → lần lượt là vectơ chỉ phương của đường thẳng d1; d2.
Áp dụng công thức ta có cosin góc giữa hai đường thẳng là:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 2 - 1 = y - 1 3 = z - 1 2 và d 2 : x = 1 - 3 t y = - 2 + t z = - 1 - t . Phương trình đường thẳng d nằm trong ( α ) : x + 2 y - 3 z - 2 = 0 và cắt hai đường thẳng d1; d2 là:
A. x + 3 5 = y - 2 - 1 = z - 1 1
B. x + 3 - 5 = y - 2 1 = z - 1 - 1
C. x - 3 - 5 = y + 2 1 = z + 1 - 1
D. x + 8 1 = y - 3 3 = z - 4
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 2 1 = y - 1 - 1 = z - 2 - 1 và d 2 : x = t y = 3 z = - 2 + t . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là.
A. x = 2 + t y = 1 + 2 t z = 2 - t
B. x = 3 + t y = 3 - 2 t z = 1 - t
C. x = 2 + 3 t y = 1 - 2 t z = 2 - 5 t
D. x = 3 + t y = 3 z = 1 - t
Trong không gian Oxyz, cho hai đường thẳng cắt nhau: d 1 : x = 1 + t, y = 1, z = 1 - t, d 2 : x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng d 1 , d 2
A. x + y + z - 3 = 0
B. x + y + z + 3 = 0
C. x - y + z - 1 = 0
D. x - y + z + 1 = 0
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d 1 : x = 1 y = 2 + t z = 2 − t và đường thẳng d 2 là giao tuyến của hai mặt phẳng P : x + y + z + 1 = 0 và Q : x − 2 y + z + 2 = 0 . Vị trí tương đối của hai đường thẳng d 1 , d 2 là
A. song song
B. cắt nhau.
C. chéo nhau.
D. trùng nhau.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và hai đường thẳng d 1 : x - 1 2 = y - 1 = z + 3 1 ; d 2 : x = 1 - t ; y = 2 t ; z = 1 . Viết phương trình đường thẳng △ đi qua A, vuông góc với cả d 1 và d 2
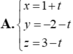
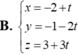
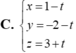

Viết phương trình đường thẳng d đi qua điểm A(-4;-5;3) và cắt cả hai đường thẳng d 1 : x + 1 3 + y + 3 - 2 = z - 2 - 1 và d 2 : x - 2 2 = y + 1 3 = z - 1 - 5
![]()
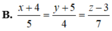
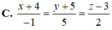
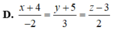
Trong không gian Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 1 3 = y + 1 2 = z - 2 - 2 , d 2 : x - 4 2 = y - 4 2 = z + 3 - 1 . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là
A. x - 4 2 = y + 1 - 1 = z 2
B. x - 2 6 = y - 2 3 = z + 2 - 2
C. x - 2 2 = y - 2 - 1 = z + 2 2
D. x - 4 2 = y - 1 - 1 = z 2