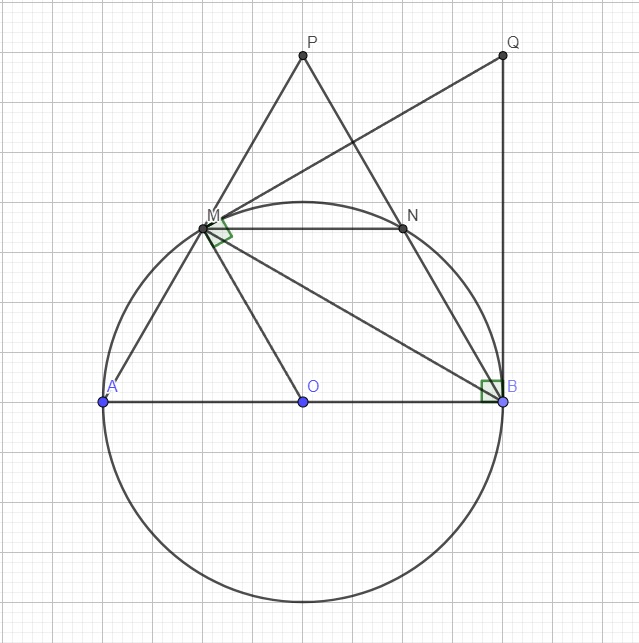
a.
Do \(AM=MN=NB\Rightarrow\widehat{AOM}=\widehat{MON}=\widehat{NOB}\)
\(\Rightarrow3\widehat{AOM}=\widehat{AOM}+\widehat{MON}+\widehat{NOB}\)
\(\Rightarrow3\widehat{AOM}=\widehat{AOB}=180^0\)
\(\Rightarrow\widehat{AOM}=\widehat{MON}=\widehat{NOB}=60^0\)
Do \(OA=OB=OM=ON=R\Rightarrow\) các tam giác AOM, MON, NOB cân
\(\Rightarrow\) Các tam giác AOM, MON, NOB là các tam giác đều (tam giác cân có 1 góc 60 độ)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{MAO}=\widehat{NBO}=60^0\left(1\right)\\\widehat{AMN}=\widehat{AMO}+\widehat{OMN}=120^0\end{matrix}\right.\)
\(\Rightarrow\widehat{MAO}+\widehat{AMN}=180^0\)
\(\Rightarrow MN||AB\) (hai góc trong cùng phía bù nhau) (2)
(1);(2)\(\Rightarrow\)AMNB là hình thang cân
b.
Ta có \(\widehat{BOM}=\widehat{BON}+\widehat{NOM}=60^0+60^0=120^0\)
Do MQ, BQ là các tiếp tuyến \(\Rightarrow\widehat{OMQ}=\widehat{OBQ}=90^0\Rightarrow\) B và M cùng nhìn OQ dưới 1 góc vuông
\(\Rightarrow OBQM\) nội tiếp
\(\Rightarrow\widehat{BOM}+\widehat{MQB}=180^0\)
\(\Rightarrow\widehat{MQB}=180^0-120^0=60^0\)
Lại có \(\widehat{OAM}=\widehat{OBN}=60^0\Rightarrow\widehat{APB}=180^0-\left(\widehat{OAM}+\widehat{OBN}\right)=60^0\)
\(\Rightarrow\widehat{APB}=\widehat{MQB}\)
c.
\(AM=MN\Rightarrow\widehat{ABM}=\widehat{NBM}=\dfrac{1}{2}\widehat{ABN}=30^0\)
\(OB=OM=R\Rightarrow\widehat{OBM}=\widehat{OMB}=30^0\)
\(\Rightarrow\widehat{BMQ}=90^0-\widehat{OMB}=60^0\)
\(\widehat{BMN}=\widehat{OBM}=30^0\) (so le trong)
\(\Rightarrow\widehat{BMN}=\dfrac{1}{2}\widehat{BMQ}\Rightarrow MN\) là phân giác của \(\widehat{BMQ}\)