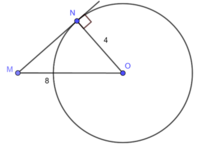
Vì MN là tiếp tuyến của đường tròn (O) tại N nên
Xét tam giác vuông MNO có:
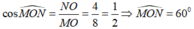
Đáp án: D

Vì MN là tiếp tuyến của đường tròn (O) tại N nên
Xét tam giác vuông MNO có:
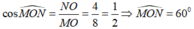
Đáp án: D
Cho đường tròn (O; 3cm) và điểm M nằm ngoài đường tròn sao cho OM = 5cm. Kẻ tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm ). Từ B kẻ đường thẳng vuông góc MO tại N cắt đường tròn (O) tại C.
a) CM: MC là tiếp tuyến của đường tròn (O).
b) Tính độ dài MN và NO.
c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chu vi tam giác MED.
d) Tính diện tích tứ giác MBOC.
Cho điểm A nằm ngoài đường tròn tâm O,kẻ hai tiếp tuyến AM,AN của đường tròn (MN là tiếp điểm).Biết góc MAN=60 độ.
a)Tính góc ở tâm MON.
b)Tính số đo các cung MN.
Cho em xin lời giải cụ thể với ạ.Em cảm ơn
Câu 4: (3,0 điểm). Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại hai điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H. a/ Tính OH. OM theo R. b/ Chứng minh: Bốn điểm M, A, I , O cùng thuộc một đường tròn. c/ Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R)
a, OI song song với AM và AB là tiếp tuyến đường tròn tâm I bán kính IO
b, MO là đường phân giác của góc AMN
c,MN là tiếp tuyến đường tròn đường kính AB
Cho đường tròn tâm ( O; R ) đường kính AB và điểm M trên đường tròn sao cho góc MAB = 60 độ. Kẻ dây MN vuông góc với AB tại H.
a) CM: AM, AN là các tiếp tuyến của đường tròn ( B; BM )
b) CM: $MN^{2}$ = 4AH.HB
c) CM: tam giác BMN là tam giác đều và điểm O là trọng tâm của nó
d) Tia MO cắt đường tròn ( O ) tại E, tia MB cắt ( B ) tại F. CM: 3 điểm N, E, F thẳng hàng
Cho đường tròn tâm ( O; R ) đường kính AB và điểm M trên đường tròn sao cho góc MAB = 60 độ. Kẻ dây MN vuông góc với AB tại H.
a) CM: AM, AN là các tiếp tuyến của đường tròn ( B; BM )
b) CM: MN2= 4AH.HB
c) CM: tam giác BMN là tam giác đều và điểm O là trọng tâm của nó
d) Tia MO cắt đường tròn ( O ) tại E, tia MB cắt ( B ) tại F. CM: 3 điểm N, E, F thẳng hàng
Cho nửa đường tròn (O) đường kính AB. Vẽ các tiếp tuyến Ax,By vè nửa mặt phẳng bờ AB chứa nửa đường tròn. Trên Ax và By theo thứ tự lấy M và N sao cho gsc MON bằng 90°.
Gọi I là trung điểm của MN. Chứng minh rằng :
a) AB là tiếp tuyến của đường tròn (I;IO)
b) MO là tia phân giác của góc AMN
Cho đường tròn ( O). Điểm M nằm ngoài đường tròn. Kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm)
a, Chứng minh OM vuông góc với AB
b, Gọi H là giao điểm của MO và AB. Kẻ đường thẳng MO cắt đường tròn ( O) lần lượt tại hai điểm P, Q ( P nằm giữa M và O). Chứng minh QH.AM=QM.AH
cho đường tròn O có bán kính là 2cm , cho A là một điểm nằm ngoài đường tròn sao cho OA=2R ( OA=4cm ) . kẻ tiếp tuyến AB , AC ( B và C là hai tiếp điểm ) . góc AOB = 60 . kẻ đường thẳng (d) đi qua A và cắt (O) tại 2 điểm P và Q bất kì . tính AP.AQ