Các câu hỏi tương tự
Cho hai hàm số y f(x), y g(x), số thực
k
∈
R
là các hàm số khả tích trên
a
;
b
⊂
R
và
c
∈
a
;
b
. Khi đó biểu thức nào sau đây là biểu thức sai.
Đọc tiếp
Cho hai hàm số y = f(x), y = g(x), số thực k ∈ R là các hàm số khả tích trên a ; b ⊂ R và c ∈ a ; b . Khi đó biểu thức nào sau đây là biểu thức sai.

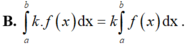
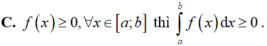
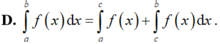
Cho số phức
z
a
+
b
i
a
,
b
∈
R
thỏa mãn
z
-
3
z
-
1
và
z
+
2...
Đọc tiếp
Cho số phức z = a + b i a , b ∈ R thỏa mãn z - 3 = z - 1 và z + 2 z - i là số thực. Tính a +b
A. -2
B. 0
C. 2
D. 4
Cho số phức z thỏa mãn
z
-
1
5
Biết tập hợp các điểm biểu diễn số phức w xác định bởi
w
2
+
3
i
.
z
+
3
+
4
i
là một đường tròn bán kính R. Tính R
Đọc tiếp
Cho số phức z thỏa mãn z - 1 = 5 Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = 2 + 3 i . z + 3 + 4 i là một đường tròn bán kính R. Tính R
![]()
![]()
![]()
![]()
Cho hai hàm số f và g liên tục trên đoạn [a;b] và số thực k bất kỳ trong R. Trong các phát biểu sau, phát biểu nào sai? A.
∫
a
b
f
x
+
g
x
d
x
∫
a
b
f
x
d
x
+
∫...
Đọc tiếp
Cho hai hàm số f và g liên tục trên đoạn [a;b] và số thực k bất kỳ trong R. Trong các phát biểu sau, phát biểu nào sai?
A. ∫ a b f x + g x d x = ∫ a b f x d x + ∫ a b g x d x
B. ∫ a b f x d x = - ∫ b a f x d x
C. ∫ a b k f x d x = k ∫ a b f x d x
D. ∫ a b x f x d x = x ∫ a b f x d x
Cho số phức z thỏa mãn
z
-
1
5
. Biết tập hợp các điểm biểu diễn số phức w xác định bởi
w
(
2
+
3
i
)
.
z
¯...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 = 5 . Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = ( 2 + 3 i ) . z ¯ + 3 + 4 i là một đường tròn bán kính R. Tính R
A. R= 5 17
B. R= 5 10
C. R= 5 5
D. R= 5 13
Cho x là số thực lớn hơn 1 và thỏa mãn
log
2
(
log
4
x
)
log
4
(
log
2
x
)
+
a
, với
a
∈
R
. Tính
P
...
Đọc tiếp
Cho x là số thực lớn hơn 1 và thỏa mãn log 2 ( log 4 x ) = log 4 ( log 2 x ) + a , với a ∈ R . Tính P = log 2 x
A. P = a 2
B. P = 2 a
C. 2 a + 1
D. P = 4 a + 1
Cho các số phức z thỏa mãn
|
z
-
4
+
3
i
|
2
. Giả sử biểu thức
P
|
z
|
đạt giá trị lớn nhất, giá trị nhỏ nhất khi z lần lượt bằng
z
1
a
1
+
b
1
i
(
a
1
,...
Đọc tiếp
Cho các số phức z thỏa mãn | z - 4 + 3 i | = 2 . Giả sử biểu thức P = | z | đạt giá trị lớn nhất, giá trị nhỏ nhất khi z lần lượt bằng z 1 = a 1 + b 1 i ( a 1 , b 1 ∈ R ) và z 2 = a 2 + b 2 i ( a 2 , b 2 ∈ R ) . Tính S = a 1 + a 2
![]()
![]()
![]()
![]()
Cho số phức z thay đổi thỏa mãn
z
-
1
1
. Biết rằng tập hợp các số phức
w
1
+
3
i
z
+
2
là đường tròn có bán kính bằng R. Tính R.
Đọc tiếp
Cho số phức z thay đổi thỏa mãn z - 1 = 1 . Biết rằng tập hợp các số phức w = 1 + 3 i z + 2 là đường tròn có bán kính bằng R. Tính R.
![]()
![]()
![]()
![]()
Cho hàm số
f
(
x
)
x
3
-
12
x
2
+
a
x
+
b
đồng biến trên R, thỏa mãn
f
f
f
3
...
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 12 x 2 + a x + b đồng biến trên R, thỏa mãn f f f 3 = 3 và f f f f 4 = 4 . Tính f(7).
A. 31.
B. 30.
C. 32.
D. 34.



