a)
\(P=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\\ =\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{4-x^2}-\dfrac{2-x}{2+x}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\\ =\left[\dfrac{\left(2+x\right)^2}{\left(2+x\right)\left(2-x\right)}+\dfrac{4x^2}{\left(2+x\right)\left(2-x\right)}-\dfrac{\left(2-x\right)^2}{\left(2+x\right)\left(2-x\right)}\right]:\dfrac{x-3}{x\left(2-x\right)}\\ =\dfrac{\left(2+x\right)^2+4x^2-\left(2-x\right)^2}{\left(2+x\right)\left(2-x\right)}:\dfrac{x-3}{x\left(2-x\right)}\\ =\dfrac{4+4x+x^2+4x^2-4+4x-x^2}{\left(2+x\right)\left(2-x\right)}\cdot\dfrac{x\left(2-x\right)}{x-3}\\ =\dfrac{4x^2+8x}{\left(2+x\right)\left(2-x\right)}\cdot\dfrac{x\left(2-x\right)}{x-3}\\ =\dfrac{4x\left(x+2\right)}{\left(2+x\right)\left(2-x\right)}\cdot\dfrac{x\left(2-x\right)}{x-3}\\ =\dfrac{4x^2}{x-3}\)
b) \(\left|x-5\right|=2\Leftrightarrow\left[{}\begin{matrix}x-5=2\left(x\ge5\right)\\x-5=-2\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\left(tm\right)\\x=3\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{4\cdot7^2}{7-3}=\dfrac{4\cdot7^2}{4}=7^2=49\)
c) \(P>0\Rightarrow\dfrac{4x^2}{x-3}>0\)
Mà: \(4x^2\ge0\forall x\)
=> \(x-3>0\Leftrightarrow x>3\)
d)
\(P=\dfrac{4x^2}{x-3}=\dfrac{4\left(x^2-6x+9\right)+24x-36}{x-3}\\ =4\left(x-3\right)+\dfrac{24x-36}{x-3}=4\left(x-3\right)+\dfrac{24\left(x-3\right)+36}{x-3}\\ =4\left(x-3\right)+\dfrac{36}{x-3}+24\)
Mà: x > 3 \(\Rightarrow\left\{{}\begin{matrix}4\left(x-3\right)>0\\\dfrac{36}{x-3}>0\end{matrix}\right.\)
Áp dụng bđt cô-si ta có:
\(P\ge2\sqrt{4\left(x-3\right)\cdot\dfrac{36}{x-3}}+24=2\sqrt{4\cdot36}+24=24+24=48\)
Dấu "=" xảy ra khi:
\(4\left(x-3\right)=\dfrac{36}{x-3}\\ \Leftrightarrow\left(x-3\right)^2=9\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\)
Vậy: ...
e)
\(P=-8\Rightarrow\dfrac{4x^2}{x-3}=-8\\ \Leftrightarrow4x^2+8\left(x-3\right)=0\\ \Leftrightarrow4x^2+8x-24=0\\ \Leftrightarrow\left(4x^2+8x+4\right)-28=0\\ \Leftrightarrow4\left(x+1\right)^2=28\\ \Leftrightarrow\left(x+1\right)^2=7\\ \Leftrightarrow\left[{}\begin{matrix}x+1=\sqrt{7}\\x+1=-\sqrt{7}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}-1\\x=-\sqrt{7}-1\end{matrix}\right.\)
a)
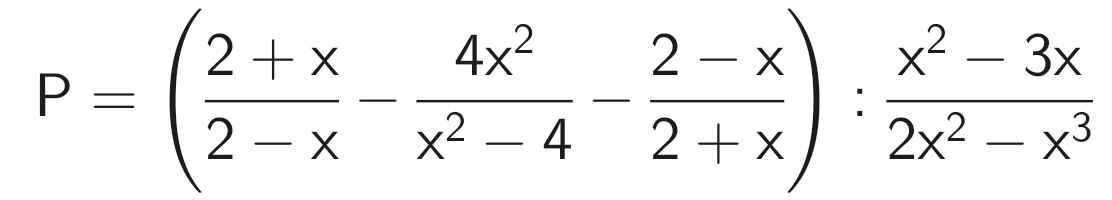
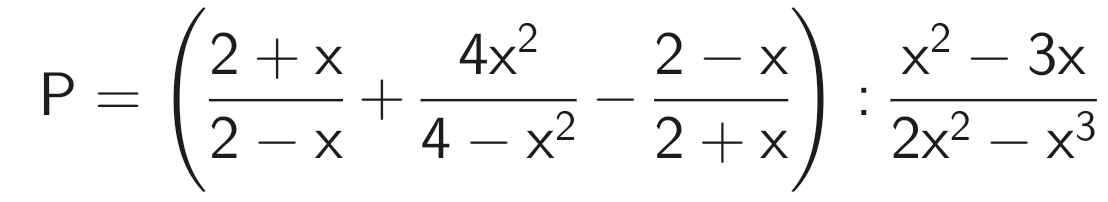
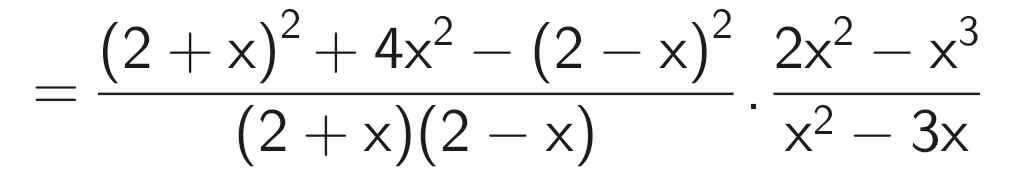
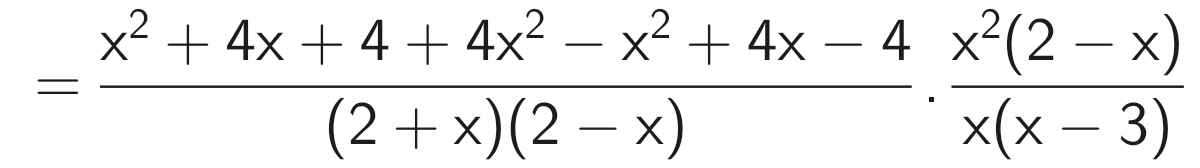
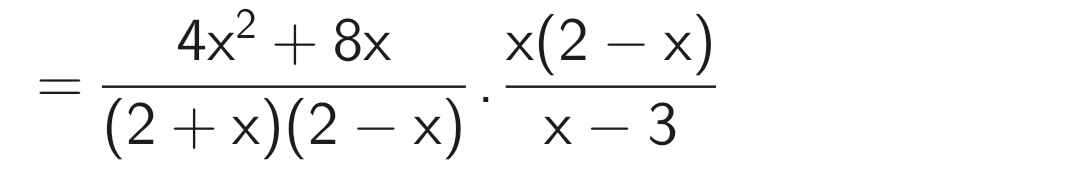
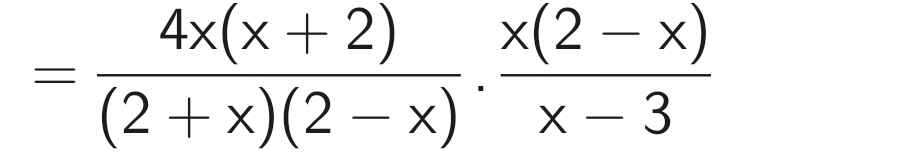
b) |x - 5| = 2
*) Với x 5, ta có:
|x - 5| = 2
x - 5 = 2
x = 2 + 5
x = 7 (nhận)
*) Với x < 5, ta có:
|x - 5| = 2
5 - x = 2
x = 5 - 2
x = 3 (nhận)
+) Với x = 7, ta có:
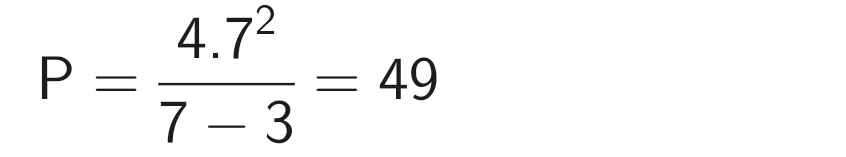+) Với x = 3, ta có mẫu thức là 3 - 3 = 0 nên P không xác định tại x = 3
