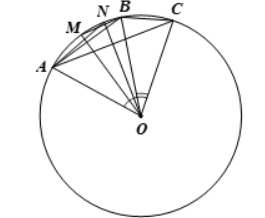
Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho \(\widehat {AOB}\)= 50o; \(\widehat {BOC}\)= 30o, điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ \(\overset\frown{AB};\overset\frown{AC}\) và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:
a) \(\widehat {BCA};\widehat {BAC}\)
b) \(\widehat {MBA};\widehat {BAN}\)
a) Ta có \(\widehat {BCA}\) và \(\widehat {AOB}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB
suy ra \(\widehat {BCA}\) = \(\frac{{\widehat {AOB}}}{2} = \frac{{{{50}^o}}}{2} = {25^o}\)
Ta có \(\widehat {BAC}\) và \(\widehat {BOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC
suy ra \(\widehat {BAC}\) = \(\frac{{\widehat {BOC}}}{2} = \frac{{{{30}^o}}}{2} = {15^o}\)
b) Ta có sđ \(\overset\frown{AB}\) = 50o ( bằng sđ của góc \(\widehat{AOB}\) cùng chắn \(\overset\frown{AB}\))
suy ra sđ \(\overset\frown{AM}=\)sđ \(\overset\frown{MB}\) = \(\frac{sđ\overset\frown{AB}}{2}=\frac{{{50}^{o}}}{2}={{25}^{o}}\) hay \(\widehat{MOA}=\widehat{MOB}={{25}^{o}}\)
Ta có \(\widehat {MBA}\) và \(\widehat {MOA}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung MA
suy ra \(\widehat {MBA}\) = \(\frac{{\widehat {MOA}}}{2} = \frac{{{{25}^o}}}{2} = 12,{5^o}\).
Ta có sđ \(\overset\frown{BC}\) = 30o ( bằng sđ của góc \(\widehat{BOC}\) cùng chắn \(\overset\frown{BC}\))
suy ra sđ \(\overset\frown{BN}=\)sđ \(\overset\frown{NC}\) = \(\frac{sđ\overset\frown{BC}}{2}=\frac{{{30}^{o}}}{2}={{15}^{o}}\) hay \(\widehat{BON}=\widehat{CON}={{15}^{o}}\)
Ta có \(\widehat {BAN}\) và \(\widehat {BON}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BN
suy ra \(\widehat {BAN}\) = \(\frac{{\widehat {BON}}}{2} = \frac{{{{15}^o}}}{2} = 7,{5^o}\).


