Ta có 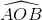 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có:
AK = OA.sin.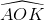 => AK = a.sin2α
=> AK = a.sin2α
OK =OA.cos.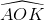 => OK = a.cos2α
=> OK = a.cos2α
Ta có 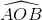 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có:
AK = OA.sin.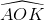 => AK = a.sin2α
=> AK = a.sin2α
OK =OA.cos.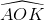 => OK = a.cos2α
=> OK = a.cos2α
Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử = α. Tính AK và OK theo a và α.
Cho Tam giac ABC cân tại A có B= 30°. Gọi H là chân đường cao kẻ từ A. Hãy xác định số đo góc giữa: (AB, AC),(AB,CB), (AB, AH),(AH,CA), (CH,HA) và kí hiệu cụ thể trên hình
Cho tan \(\alpha\)- 3cot \(\alpha\) = 2 và π/2 < α < π
Tìm \(\sin\alpha,\cos\alpha\)
Cho \(\sin\alpha=\sqrt{3}\cos\alpha\) và 0 < π < π/2
Tìm \(\sin\alpha,\cos\alpha\)
Với những giá trị nào của góc \(\alpha\) (\(0^0\le\alpha\le180^0\)) thì :
a) \(\sin\alpha\) và \(\cos\alpha\) cùng dấu ?
b) \(\sin\alpha\) và \(\cos\alpha\) khác dấu ?
c) \(\sin\alpha\) và \(\tan\alpha\) cùng dấu ?
d) \(\sin\alpha\) và \(\tan\alpha\) khác dấu ?
Cho \(\cos\alpha=-\dfrac{\sqrt{2}}{4}\). Tính \(\sin\alpha\) và \(\tan\alpha\) ?
Cho \(\tan\alpha=-2\sqrt{2}\) với \(0^0< \alpha< 90^0\). Tính \(\sin\alpha\) và \(\cos\alpha\) ?
Cho \(\sin\alpha=\dfrac{1}{4}\) với \(90^0< \alpha< 180^0\). Tính \(\cos\alpha\) và \(\tan\alpha\) ?
Tính giá trị của hàm số lượng giác:
\(\tan\alpha+\cot\alpha=2\) ; \(0< \alpha< \dfrac{\pi}{2}\)