Các câu hỏi tương tự
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây? A. Phép tịnh tiến theo vectơ
A
G
→
B. Phép vị tự tâm A tỉ số
2
3
C. Phép vị tự tâm M tỉ số
1
3...
Đọc tiếp
∆ABC có 2 điểm B, C cố định, A chạy trên đường tròn (C) tâm O bán kính R. Biết (C) không qua B, C. Gọi M là trung điểm của BC, G là trọng tâm ∆ABC. Khi A chạy trên (C) thì G chạy trên đường tròn (C’) là ảnh của (C) qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ A G →
B. Phép vị tự tâm A tỉ số 2 3
C. Phép vị tự tâm M tỉ số 1 3
D. Phép tịnh tiến theo vectơ M G →
vẽ tam giác ABC vuông tại A có đường cao AH.
a) C/m t/g ABH~t/g CBA.
b) Tính BC, AH, BH. Biết AB= 15cm, AC=20cm.
c) Gọi E, F l;à 2 điểm đối xứng của H qua AB và AC. Tính dt tứ giác EFCB
Câu 1:(0,5đ)Liệt kê các phần tử của tập hợp A {x ∈ N/15 ≤ x ≤ 19}Câu 2: (3đ) thực hiện phép tínha. 2.(72 – 2.32) – 60b. 27.63 + 27.37c. l-7l + (-8) + l-11l + 2d. 568 – 34 {5.l9 – ( 4-1)2l + 10}Câu 3: ( 2,5 điểm ) Tìm số nguyên xa) 2x + 3 52 : 5b) 105 – ( x + 7) 27 : 25Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ...
Đọc tiếp
Câu 1:(0,5đ)
Liệt kê các phần tử của tập hợp A = {x ∈ N/15 ≤ x ≤ 19}
Câu 2: (3đ) thực hiện phép tính
a. 2.(72 – 2.32) – 60
b. 27.63 + 27.37
c. l-7l + (-8) + l-11l + 2
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
Câu 3: ( 2,5 điểm ) Tìm số nguyên x
a) 2x + 3 = 52 : 5
b) 105 – ( x + 7) = 27 : 25
Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.
Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ hình minh họa.
Câu 6: ( 2 điểm )Vẽ tia Ox, trên Ox lấy điểm A và B sao cho OA= 4cm, OB = 8cm.
a. Trong 3 điểm O, A, B điểm nào nằm giữa 2 điểm còn lại. Vì sao? . So sánh OA và AB
b. A có phải là trung điểm của OB không? Vì sao ?
13/04 lúc 19:56
1.Tìm nghiệm của đa thức sau: h(y)=y^2-|y|
2.Cho g(x)=ax^2+bx+c có a,b,c thỏa mãn:3a+b=0
CMR:g(1).g(2) >= 0
giúp tớ nha!
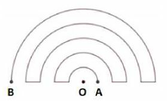
Gọi L là chiều dài của đoạn đường có điểm đầu là A và điểm cuối B (hình vẽ là những nửa đường tròn đồng tâm O và có bán kính lần lượt là 1, 2, 3, 4, 5). Hãy chọn khẳng định đúng. A. 51 B. L 52 C. 47 D. L 50
Đọc tiếp
Gọi L là chiều dài của đoạn đường có điểm đầu là A và điểm cuối B (hình vẽ là những nửa đường tròn đồng tâm O và có bán kính lần lượt là 1, 2, 3, 4, 5). Hãy chọn khẳng định đúng.
A. 51
B. L > 52
C. 47
D. L < 50
Cho hai đa thức
f(x)=3x2-x2+x-7+x4+6x3
g(x)= -2x2-4x4+6+4x2-6x3-x
a)Thu gọn và sắp xếp đa thức trên theo lũy thừa giảm dần của biến
b)Tính h(x)=g(x)+g(x)
c)Tìm nghiệm của đa thức h(x)
(mình cần chủ yếu là câu C)
Trong không gian Oxyz, cho tam giác OAB với O(0;0;0),A(6;0;0),B(0;8;0). Điểm M(a;b;c)thuộc mặt phẳng (P): x+2y+3z-20 đồng thời cách đều các đỉnh O, A, B. Giá trị của tổng a+b-c là A. -2. B. 2. C. 4. D. 10
Đọc tiếp
Trong không gian Oxyz, cho tam giác OAB với O(0;0;0),A(6;0;0),B(0;8;0). Điểm M(a;b;c)thuộc mặt phẳng (P): x+2y+3z-2=0 đồng thời cách đều các đỉnh O, A, B. Giá trị của tổng a+b-c là
A. -2.
B. 2.
C. 4.
D. 10
Cho mặt cầu S(O;R) và (P) cách O một khoảng bằng h (0hR). Gọi (L) là đường tròn giao tuyến của mặt cầu (S) và (P) có bán kính r. Lấy A là một điểm cố định thuộc (L). Một góc vuông xAy trong (P) quay quanh điểm A. Các cạnh Ax, Ay cắt (L) ở C và D. Đường thẳng đi qua A và vuông góc với (P) cắt mặt cầu ở B. Diện tích ΔBCD lớn nhất bằng A.
2
r
r
2
+
4
h...
Đọc tiếp
Cho mặt cầu S(O;R) và (P) cách O một khoảng bằng h (0<h<R). Gọi (L) là đường tròn giao tuyến của mặt cầu (S) và (P) có bán kính r. Lấy A là một điểm cố định thuộc (L). Một góc vuông xAy trong (P) quay quanh điểm A. Các cạnh Ax, Ay cắt (L) ở C và D. Đường thẳng đi qua A và vuông góc với (P) cắt mặt cầu ở B. Diện tích ΔBCD lớn nhất bằng
A. 2 r r 2 + 4 h 2
B. r r 2 + 4 h 2
C. r r 2 + h 2
D. 2 r r 2 + h 2
rút gọn biểu thức : a) ( a-4) (a+5) - (a-5) (a+4) b) (2-a) (a+7) - (a-1) (a+2)
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm O(0;0;0), A(0;1;-2), B(1;2;1), C(4;3;m). Giá trị m để 4 điểm O, A, B, C đồng phẳng là
A. -7
B. -14
C. 14
D. 7