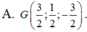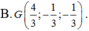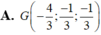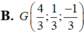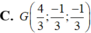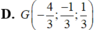a:
A(-2;0;3); B(1;4;-2); C(1;-2;1)
=>\(\overrightarrow{AB}=\left(3;4;-5\right);\overrightarrow{AC}=\left(3;-2;-2\right)\)
Vì \(\dfrac{3}{3}\ne\dfrac{4}{-2}\ne\dfrac{-5}{-2}\)
nên A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của một tam giác
b: \(AB=\sqrt{\left(1+2\right)^2+\left(4-0\right)^2+\left(-2-3\right)^2}=5\sqrt{2}\)
\(BC=\sqrt{\left(1-1\right)^2+\left(-2-4\right)^2+\left(1+2\right)^2}=3\sqrt{5}\)
\(AC=\sqrt{\left(1+2\right)^2+\left(-2-0\right)^2+\left(1-3\right)^2}=\sqrt{17}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=3\sqrt{5}+5\sqrt{2}+\sqrt{17}\)
c: Tọa độ trung điểm I của AB là:
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-2+1}{2}=-\dfrac{1}{2}\\y_I=\dfrac{0+4}{2}=\dfrac{4}{2}=2\\z_I=\dfrac{3+1}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
=>I(-1/2;2;2)
d: Tọa độ trọng tâm G của ΔABC là:
\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-2+1+1}{3}=0\\y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{0+4+\left(-2\right)}{3}=\dfrac{2}{3}\\z_G=\dfrac{z_A+z_B+z_C}{3}=\dfrac{3+\left(-2\right)+1}{3}=\dfrac{2}{3}\end{matrix}\right.\)
=>\(G\left(0;\dfrac{2}{3};\dfrac{2}{3}\right)\)
e: Xét ΔABC có
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{50+17-45}{2\cdot5\sqrt{2}\cdot\sqrt{17}}=\dfrac{22}{10\sqrt{34}}\)
=>\(\widehat{BAC}\simeq68^0\)
f: M đối xứng C qua B
=>B là trung điểm của CM
=>\(\left\{{}\begin{matrix}x_M+x_C=2\cdot x_B\\y_M+y_C=2\cdot y_B\\z_M+z_C=2\cdot z_B\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=2\cdot1-1=1\\y_M=2\cdot4-2\cdot\left(-2\right)=12\\z_M=2\cdot\left(-2\right)-1=-5\end{matrix}\right.\)
=>M(1;12;-5)