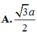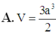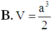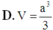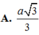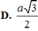Do \(SH\perp\left(ABCD\right)\) nên \(\widehat{SHB}=\widehat{SHA}=\widehat{SHC}=90^0\). Mà ta có \(HB=HA=HC\left(=a\sqrt{2}\right)\) nên \(\Delta HAS=\Delta HCS=\Delta HBS\), suy ra \(SA=SB=SC\).
Đặt \(x=SH\Rightarrow SA=SB=SC=\sqrt{SH^2+AH^2}=\sqrt{x^2+2a^2}\)
Trong (SBC), đường thẳng qua B vuông góc BC cắt SC tại M. Khi đó \(\left(\left(SBC\right),\left(ABCD\right)\right)=\widehat{ABM}=60^0\).
Xét trên (SBC): \(cos\widehat{BCS}=\dfrac{BC^2+SC^2-BS^2}{2BC.SC}=\dfrac{BC}{2SC}=\dfrac{a}{\sqrt{x^2+2a^2}}\)
\(\Rightarrow tan\widehat{BCS}=\sqrt{\dfrac{1}{cos^2\widehat{BCS}}-1}=\sqrt{\dfrac{x^2+2a^2}{a^2}-1}=\dfrac{\sqrt{x^2+a^2}}{a}\)
\(\Rightarrow\left\{{}\begin{matrix}BM=tan\widehat{BCS}.BC=2\sqrt{x^2+a^2}\\CM=\dfrac{BC}{cos\widehat{BCS}}=2\sqrt{x^2+2a^2}\end{matrix}\right.\)
Xét trên (ASC): \(cos\widehat{ACS}=\dfrac{AC^2+CS^2-AS^2}{2AC.CS}=\dfrac{AC}{2SC}=\sqrt{\dfrac{2}{x^2+2a^2}}a\)
\(\Rightarrow AM=\sqrt{AC^2+CM^2-2cos\widehat{ACS}.AC.CM}\)
\(=\sqrt{8a^2+4\left(x^2+2a^2\right)-2.a\sqrt{\dfrac{2}{x^2+2a^2}}.2\sqrt{x^2+2a^2}.2a\sqrt{2}}\)
\(\sqrt{8a^2+4\left(x^2+2a^2\right)-16a^2}=2x\)
Vậy \(AM^2+AB^2=BM^2\), do đó tam giác ABM vuông tại A.
\(\Rightarrow AM=tan60^0.AB=2a\sqrt{3}=2x\Rightarrow x=a\sqrt{3}\).
\(\Rightarrow SH=a\sqrt{3};SA=SB=SC=a\sqrt{5}\)
a) Từ H hạ HN vuông góc AB tại N (N thuộc (ABC)), HP vuông góc AS tại P (P thuộc (SAC)).
Khi đó, N là trung điểm AB, và: \(SP=\dfrac{SH^2}{AS}=\dfrac{3a^2}{a\sqrt{5}}=\dfrac{3a}{\sqrt{5}}\); \(HP=\dfrac{AH.HS}{AS}=\dfrac{a\sqrt{2}.a\sqrt{3}}{a\sqrt{5}}=a\sqrt{\dfrac{6}{5}}\)
Trên (SAB), đường thẳng qua P vuông góc SA cắt đường thẳng qua N vuông góc AB.
Ta có: \(TP\perp AS;HP\perp AS\Rightarrow HT\perp AS\) ; \(TN\perp AB;HN\perp AB\Rightarrow HT\perp AB\)
\(\Rightarrow HT\perp\left(SAB\right)\Rightarrow d\left(H,\left(SAB\right)\right)=HT\) và \(HT\perp TP\) tại T; \(HN=a\).
Do tam giác SAB cân tại S nên T thuộc SN. Khi đó \(\Delta SPT\sim\Delta SNA\).
Có: \(cos\widehat{SAB}=\dfrac{SA^2+AB^2-SB^2}{2SA.AB}=\dfrac{AB}{2SA}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow sin\widehat{SAN}=\dfrac{2}{\sqrt{5}}\Rightarrow SN=sin\widehat{SAB}.AS=\dfrac{2}{\sqrt{5}}.a\sqrt{5}=2a\)
\(\Rightarrow TP=AN.\dfrac{SP}{SN}=a.\dfrac{\dfrac{3a}{\sqrt{5}}}{2a}=\dfrac{3}{2\sqrt{5}}a\)
\(\Rightarrow HT=\sqrt{HP^2-TP^2}=\sqrt{\dfrac{6}{5}a^2-\dfrac{9}{20}a^2}=\dfrac{a\sqrt{3}}{2}\)