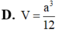Diện tích tam giác SBC là \(\frac{a^2\sqrt3}{4}\)
=>\(\frac12\cdot SB\cdot SC\cdot\sin BSC=\frac{a^2\sqrt3}{4}\)
=>\(\frac12\cdot a\cdot a\sqrt3\cdot\sin BSC=\frac{a^2\sqrt3}{4}\)
=>\(\frac{a^2\sqrt3}{2}\cdot\sin BSC=\frac{a^2\sqrt3}{4}\)
=>\(\sin BSC=\frac12\)
=>\(\hat{BSC}=30^0\)
Xét ΔSBC có \(cosBSC=\frac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}\)
=>\(\frac{a^2+\left(a\sqrt3\right)^2-BC^2}{2\cdot a\cdot a\sqrt3}=cos30=\frac{\sqrt3}{2}\)
=>\(4a^2-BC^2=2a^2\sqrt3\cdot\frac{\sqrt3}{2}=3a^2\)
=>\(BC^2=a^2\)
=>BC=a
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(AB^2=a^2-\left(\frac{a\sqrt7}{4}\right)^2=a^2-a^2\cdot\frac{7}{16}=\frac{9}{16}a^2=\left(\frac34a\right)^2\)
=>\(AB=\frac34a\)
ΔSAC vuông tại A
=>\(SA^2+AC^2=SC^2\)
=>\(AC^2=\left(a\sqrt3\right)^2-\left(\frac{a\sqrt7}{4}\right)^2=3a^2-\frac{7a^2}{16}=\frac{41a^2}{16}\)
=>\(AC=\frac{a\sqrt{41}}{4}\)
Xét ΔABC có AM là đường trung tuyến
nên \(AM^2=\frac{AB^2+AC^2}{2}-\frac{BC^2}{4}\)
\(=\frac{\frac{9}{16}a^2+\frac{41}{16}a^2}{2}-\frac{a^2}{4}=\frac{\frac{25}{8}a^2}{2}-\frac{a^2}{4}=\frac{25}{16}a^2-\frac{a^2}{4}=\frac{21}{16}a^2\)
=>\(AM=\frac{a\sqrt{21}}{4}\)
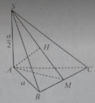
\(\hat{SM;\left(ABC\right)}=\hat{MS;MA}=\hat{SMA}\)
Xét ΔSMA vuông tại A có tan SMA\(=\frac{SA}{AM}=\frac{a\sqrt7}{4}:\frac{a\sqrt{21}}{4}=\frac{\sqrt7}{\sqrt{21}}=\frac{1}{\sqrt3}\)
nên \(\hat{SMA}=30^0\)
=>\(\hat{SM;\left(ABC\right)}=30^0\)