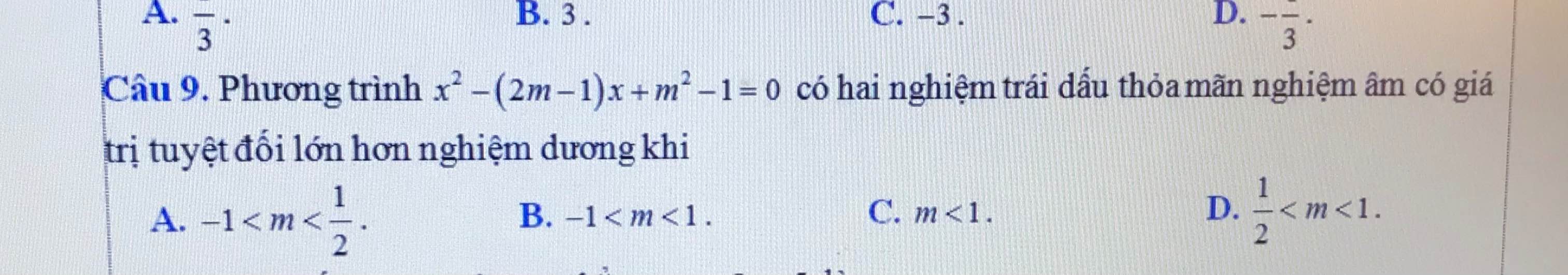a: \(A=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\sqrt{x}+1+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\)
b: \(P=A\cdot B=\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}\cdot\dfrac{2}{\sqrt{x}-1}=\dfrac{2}{x+\sqrt{x}+1}\)
c: Khi x=4 thì \(P=\dfrac{2}{4+2+1}=\dfrac{2}{7}\)
d: \(P=\dfrac{2}{3\sqrt{x}+1}\)
=>\(x+\sqrt{x}+1=3\sqrt{x}\)
=>\(x-2\sqrt{x}=0\)
=>\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
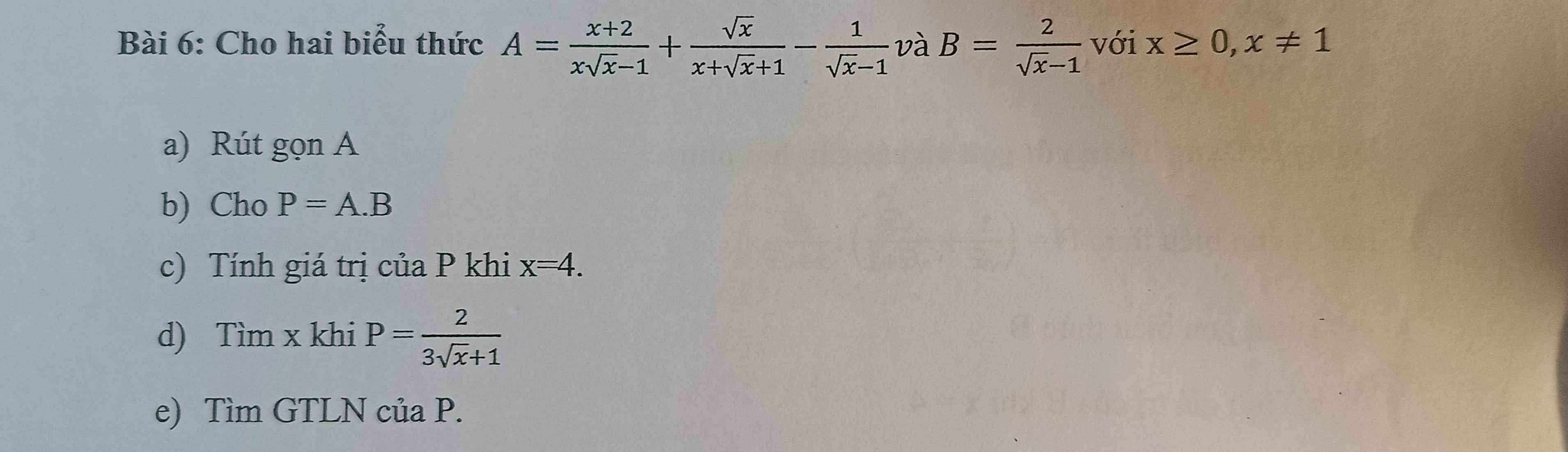
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Giúp mình giải chi tiết nha
