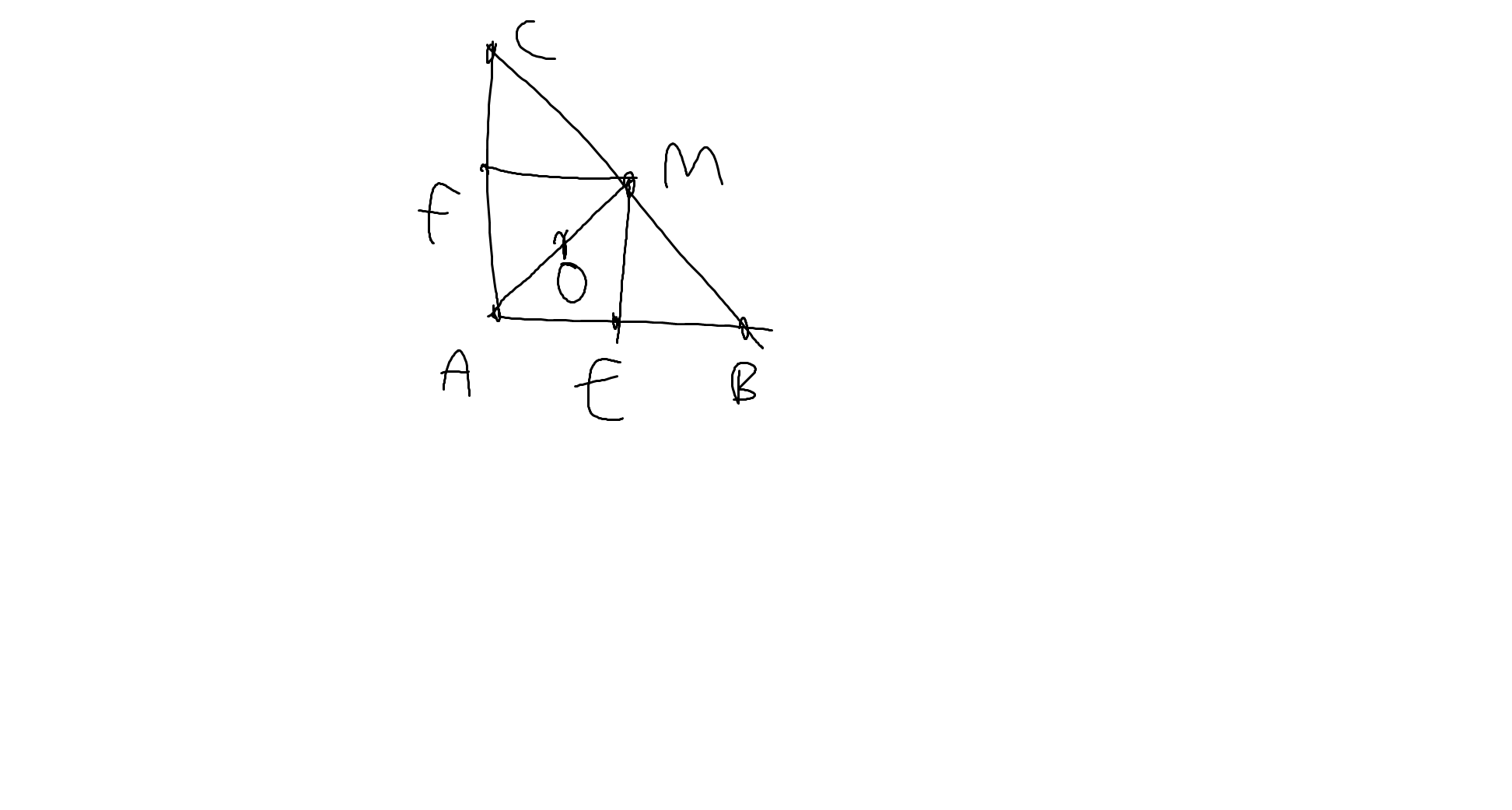
Bài 6 : [ bài này vẽ hình giúp e với ạ ] Cho tam giác ABC vuông tại A , M là trung điểm của BC . Từ M kẻ ME // AC ( E thuộc AB ) và MF // AB ( F thuộc AC ).
a, Chứng minh tứ giác AEMF là hình chữ nhật.
b, Chứng minh tam giác EBM = tam giác FMC.
c, tứ giác BEFM là hình gì ? vì sao ?
d, Gọi O là trung điểm của AB . Chứng minh OE = OF
Bài 8 : [ bài này vẽ hình giúp e với ạ ] Cho tam giác ABC vuông tại A có AB < AC . Gọi M là trung điểm của BC . Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, Chứng minh ABCD là hình chữ nhật.
b, Lấy điểm E sao cho B là trung điểm của AE . chứng minh BE = DC và BEDC là hình bình hành.
Bài 4 : Cho hình chữ nhật ABCD . gọi M , N là trung điểm của AB , CD.
a, chứng minh AMND là hình chữ nhật.
b, chứng minh MBND là hình chữ nhật.
Bài 9 : [ bài này vẽ hình giúp e với ạ ] Cho tam giác ABC vuông tại A có AB < AC . N là trung điểm BC . GỌi M, P lần lượt là chân đường vuông góc của N trên AB,AC . Lấy E sao cho P là trung điểm của NE.
a, Chứng minh NPAM là hình chữ nhật.
b, Chứng minh tam giác MBN = tam giác PNC , từ đó chứng minh P là trung điểm của AC.
c, Tứ giác ANCE là hình gì ? Vì sao ?
Bài 6: Sửa đề: O là trung điểm của AM
a: Xét tứ giác AEMF có
AE//MF
AF//ME
Do đó: AEMF là hình bình hành
Hình bình hành AEMF có \(\widehat{EAF}=90^0\)
nên AEMF là hình chữ nhật
b: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Ta có: AE=EB
FM=AE
Do đó: FM=EB
Xét ΔBEM vuông tại E và ΔMFC vuông tại F có
BM=MC
BE=MF
Do đó: ΔBEM=ΔMFC
c: Xét tứ giác BEFM có
BE//FM
BE=FM
Do đó: BEFM là hình bình hành
d: Ta có: AEMF là hình chữ nhật
=>AM cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AM
nên O là trung điểm của EF
=>OE=OF
Bài 8:
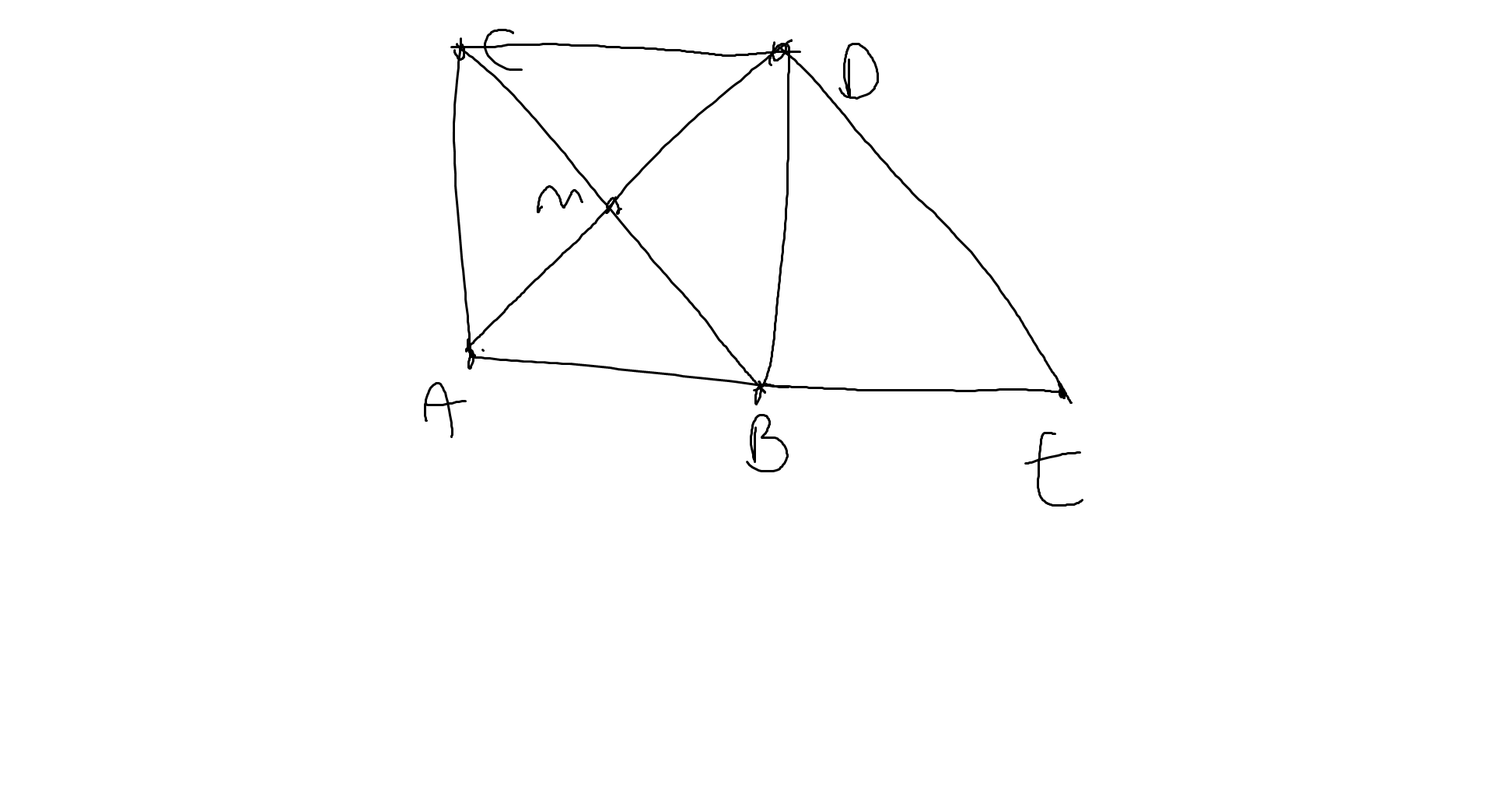
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: ABDC là hình chữ nhật
=>AB//DC và AB=DC
Ta có: AB//DC
=>BE//CD
Ta có: AB=DC
AB=BE
Do đó: DC=BE
Xét tứ giác BEDC có
BE//DC
BE=DC
Do đó: BEDC là hình bình hành
Bài 9:
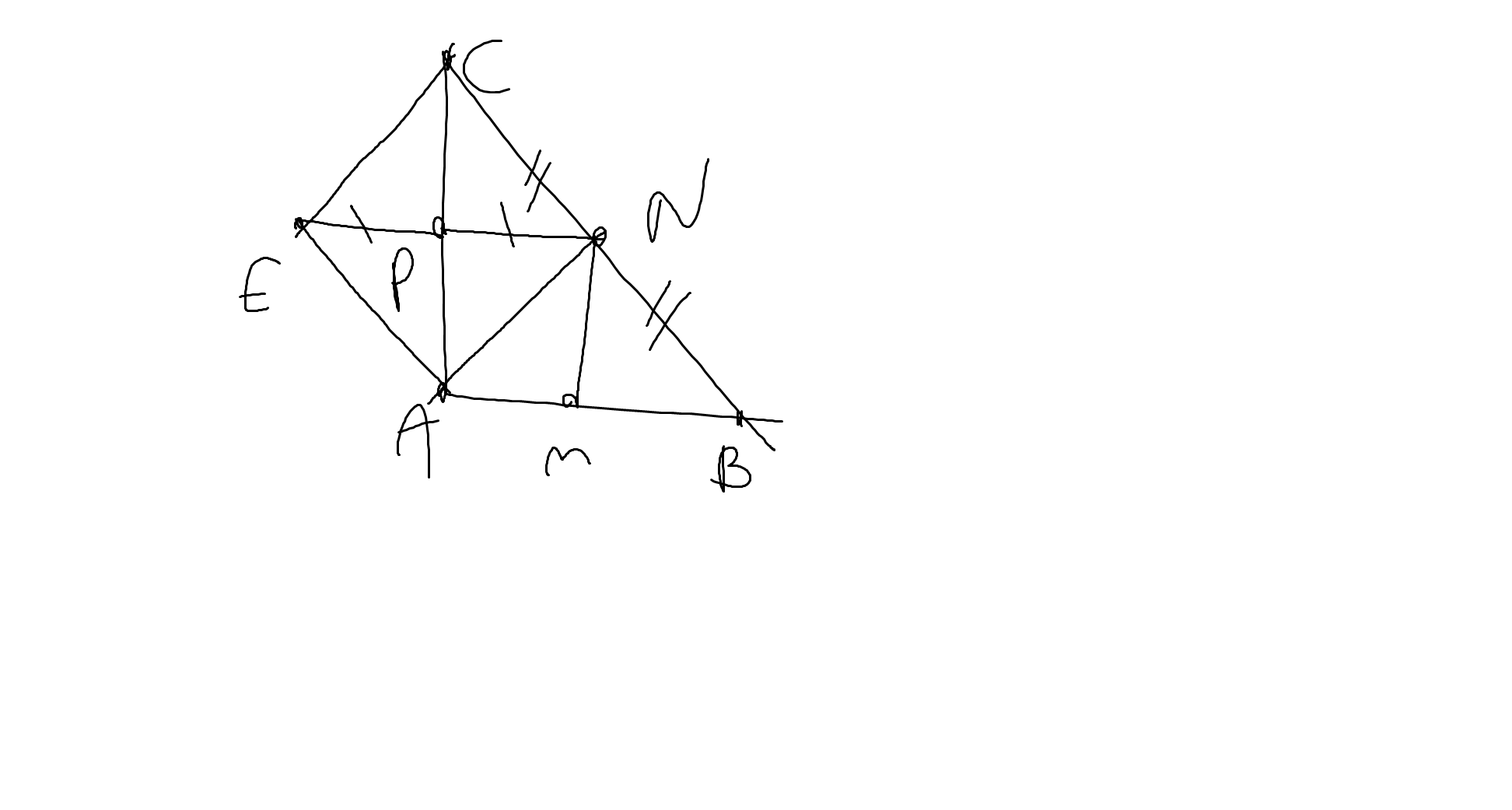
a: Xét tứ giác AMNP có \(\widehat{AMN}=\widehat{APN}=\widehat{PAM}=90^0\)
nên AMNP là hình chữ nhật
b: Xét ΔABC có
N là trung điểm của BC
NP//AB
Do đó: P là trung điểm của AC
Xét ΔABC có
N là trung điểm của BC
NM//AC
Do đó: M là trung điểm của AB
=>MA=MB
mà MA=NP
nên NP=MB
Xét ΔBMN vuông tại M và ΔNPC vuông tại P có
BN=NC
BM=NP
Do đó: ΔBMN=ΔNPC
c: Xét tứ giác ANCE có
P là trung điểm chung của AC và NE
=>ANCE là hình bình hành
Hình bình hành ANCE có AC\(\perp\)NE
nên ANCE là hình thoi














