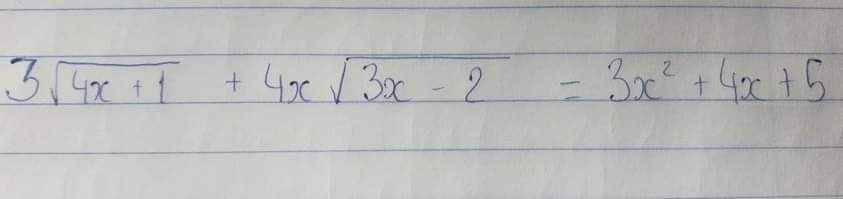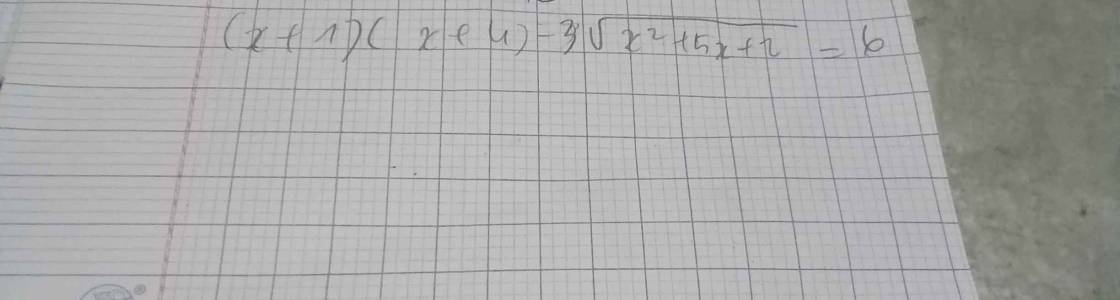giải giúp e vs ạ e đag gấppp
**BÀI 5:** Cho tam giác \(ABC\) vuông tại \(A\) \((AB < AC)\), đường cao \(AH\)
a) Cho \(AB = 6 \, \text{cm}\) và \(\cos\) góc \(ABC = \frac{3}{5}\). Tính \(BC, AC, BH\)
b) Kẻ \(HD \perp AB\) tại \(D\), \(HE \perp AC\) tại \(E\). Chứng minh \(AD \cdot AB = AE \cdot AC\)
c) Gọi \(I\) là trung điểm \(BC\), \(AI\) cắt \(DE\) tại \(K\). Chứng minh rằng \(AK \perp ED\)
a:
Xét ΔABC vuông tại A có \(cosABC=\frac{BA}{BC}\)
=>\(\frac{6}{BC}=\frac35\)
=>\(BC=6\cdot\frac53=10\left(\operatorname{cm}\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=100-36=64=8^2\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH=\frac{6^2}{10}=3,6\left(\operatorname{cm}\right)\)
b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)
c: ΔABC vuông tại A
mà AI là đường trung tuyến
nên IA=IC
=>ΔIAC cân tại I
=>\(\hat{IAC}=\hat{ICA}\)
AEHD là hình chữ nhật
=>\(\hat{AED}=\hat{AHD}\)
mà \(\hat{AHD}=\hat{ABC}\left(=90^0-\hat{HAB}\right)\)
nên \(\hat{AED}=\hat{ABC}\)
\(\hat{IAC}+\hat{AED}=\hat{ICA}+\hat{ABC}=90^0\)
=>AI⊥ED tại K