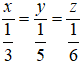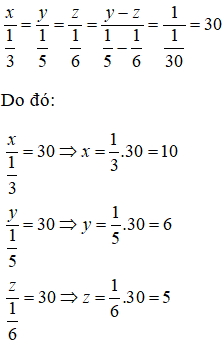Bài 29:
Ta có: y=f(x)=x2−2y=f(x)=x2−2
Thay x=2;1;0;−1;−2x=2;1;0;−1;−2 vào hàm số ta được:
f(2)=22−2=4−2=2f(2)=22−2=4−2=2
f(1)=12−2=1−2=−1f(1)=12−2=1−2=−1
f(0)=02−2=−2f(0)=02−2=−2
f(−1)=(−1)2−2=1−2=−1f(−1)=(−1)2−2=1−2=−1
f(−2)=(−2)2−2=4−2=2
Bài 30:
Hàm số y=f(x)=1–8xy=f(x)=1–8x
a) f(−1)=1−8.(−1)=1+8=9f(−1)=1−8.(−1)=1+8=9 nên khẳng định f(−1)=9f(−1)=9 đúng.
b) f(12)=1−8.12=1−4=−3f(12)=1−8.12=1−4=−3
⇒ Khẳng định f(12)=−3f(12)=−3 đúng.
c) f(3)=1−8.3=1−24=−23≠25f(3)=1−8.3=1−24=−23≠25 nên khẳng định f(3)=25 f(3)= 25 sai.
29. Gọi x(s), y(s), z(s) lần lượt là thời gian chạy hết quãng đường của Chó, Mèo, Gà. (x > 0; y > 0; z > 0).
Vì độ dài quãng đường bằng nhau nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch
Ta có: x.10 = y.8 = z.4 = 80.1
Suy ra: x .10 = 80 nên x = 80 : 10 = 8
y.8 = 80 nên y = 80 : 8 = 10
z.4 = 80 nên z = 80 : 4 = 20
Vậy Chó chạy 100m hết 8s, Mèo hết 10s và Gà hết 20s
Thành tích của toàn đội tuyển là:
8 + 10 + 20 + 80 = 118s
30.
Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện x, y, z ∈ N*)
Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z.
Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1.
Từ 3x = 5y = 6z, suy ra
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy
giúp mik làm bài 2 và 3 đi
