giup mình với
Giải:
a) \(\left(x+1\right)^2-\left(x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[\left(x+1\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+1-x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)3=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy ...
b) \(4x\left(x-2017\right)-x+2017=0\)
\(\Leftrightarrow4x\left(x-2017\right)-\left(x-2017\right)=0\)
\(\Leftrightarrow\left(x-2017\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2017=0\\4x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy ...
c) \(\left(x+1\right)^2=x+1\)
\(\Leftrightarrow\left(x+1\right)^2-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+1-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy ...
Chúc bạn học tốt!
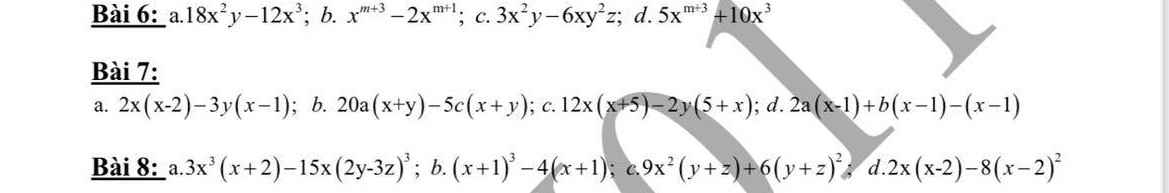giúp mình nhanh với mình sắp học rồi.Camon các bạn rất nhìu :>>
