a.
\(\Leftrightarrow\left(x+1\right)^2+2\left(x^2+3\right)=3\left(x+1\right)\sqrt{x^2+3}\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{x^2+3}=b\end{matrix}\right.\) ta được:
\(a^2+2b^2=3ab\)
\(\Leftrightarrow\left(a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=2b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+3}=x+1\\2\sqrt{x^2+3}=x+1\end{matrix}\right.\) (\(x\ge-1\))
\(\Rightarrow\left[{}\begin{matrix}x^2+3=x^2+2x+1\\4\left(x^2+3\right)=x^2+2x+1\end{matrix}\right.\) (\(x\ge-1\))
\(\Rightarrow...\)
b.
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow x^2+1-\sqrt{x\left(x^2+1\right)}-3x=0\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+1}=a>0\\\sqrt{x}=b\ge0\end{matrix}\right.\)
\(\Rightarrow a^2-ab-3b^2=0\) (đề cho hệ số không hợp lý chút xíu nào)
\(\Leftrightarrow\left(a-\dfrac{1+\sqrt{13}}{2}b\right)\left(a+\dfrac{\sqrt{13}-1}{2}b\right)=0\)
\(\Leftrightarrow a=\dfrac{1+\sqrt{13}}{2}b\)
\(\Leftrightarrow\sqrt{x^2+1}=\dfrac{1+\sqrt{13}}{2}\sqrt{x}\)
\(\Leftrightarrow x^2+1=\dfrac{7+\sqrt{13}}{2}x\)
\(\Leftrightarrow x^2-\dfrac{7+\sqrt{13}}{2}x+1=0\)
Tới đây em chịu khó tính delta bằng tay rồi tính nghiệm
c.
ĐKXĐ: \(x\ge-1\)
\(x^2+5x+7=7\sqrt{\left(x+1\right)\left(x^2-x+1\right)}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\ge0\\\sqrt{x^2-x+1}=b>0\end{matrix}\right.\)
\(a^2+6b^2=7ab\)
\(\Leftrightarrow\left(a-b\right)\left(a-6b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=6b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+1}=\sqrt{x^2-x+1}\\\sqrt{x+1}=6\sqrt{x^2-x+1}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=x^2-x+1\\x+1=36\left(x^2-x+1\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
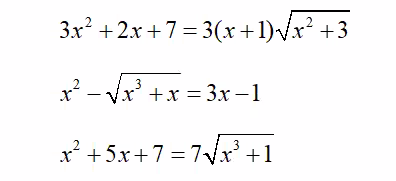
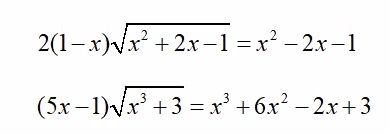
mn giúp em với em cần gấp bài 2 nha thank you 
