`x-4+sqrt{x-2}=0(x>=2)`
`<=>x-2+sqrt{x-2}-2=0`
Đặt `a=sqrt{x-2}(a>=0)`
`pt<=>a^2+a-2=0`
`a+b+c=0`
`=>a_1=1,a_2=c/2-2(l)`
`=>sqrt{x-2}=1`
`=>x-2=1`
`=>x=3(tm)`
Vậy `S={3}`
x - 4 + \(\sqrt{x-2}\) = 0
⇔ \(\sqrt{x-2}\) = 4 - x ( x≤ 4)
⇔ x - 2 = (4 - x)2
⇔ x - 2 = 16 - 8x + x2
⇔ x2 - 9x + 18 = 0
⇔ \(\left[{}\begin{matrix}x=6\left(ktm,loại\right)\\x=3\left(tm\right)\end{matrix}\right.\)
Vậy x=3 là gtct

 ai giúp mình với ạ
ai giúp mình với ạ










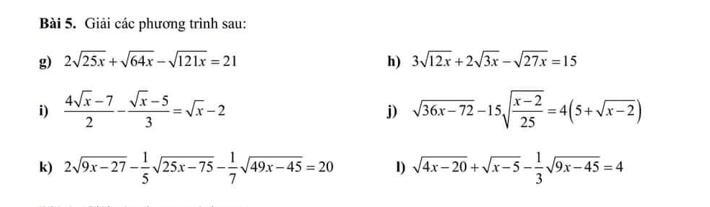








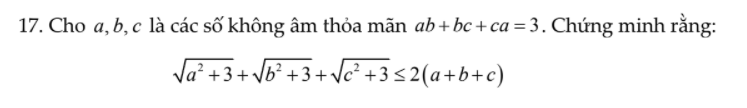 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.