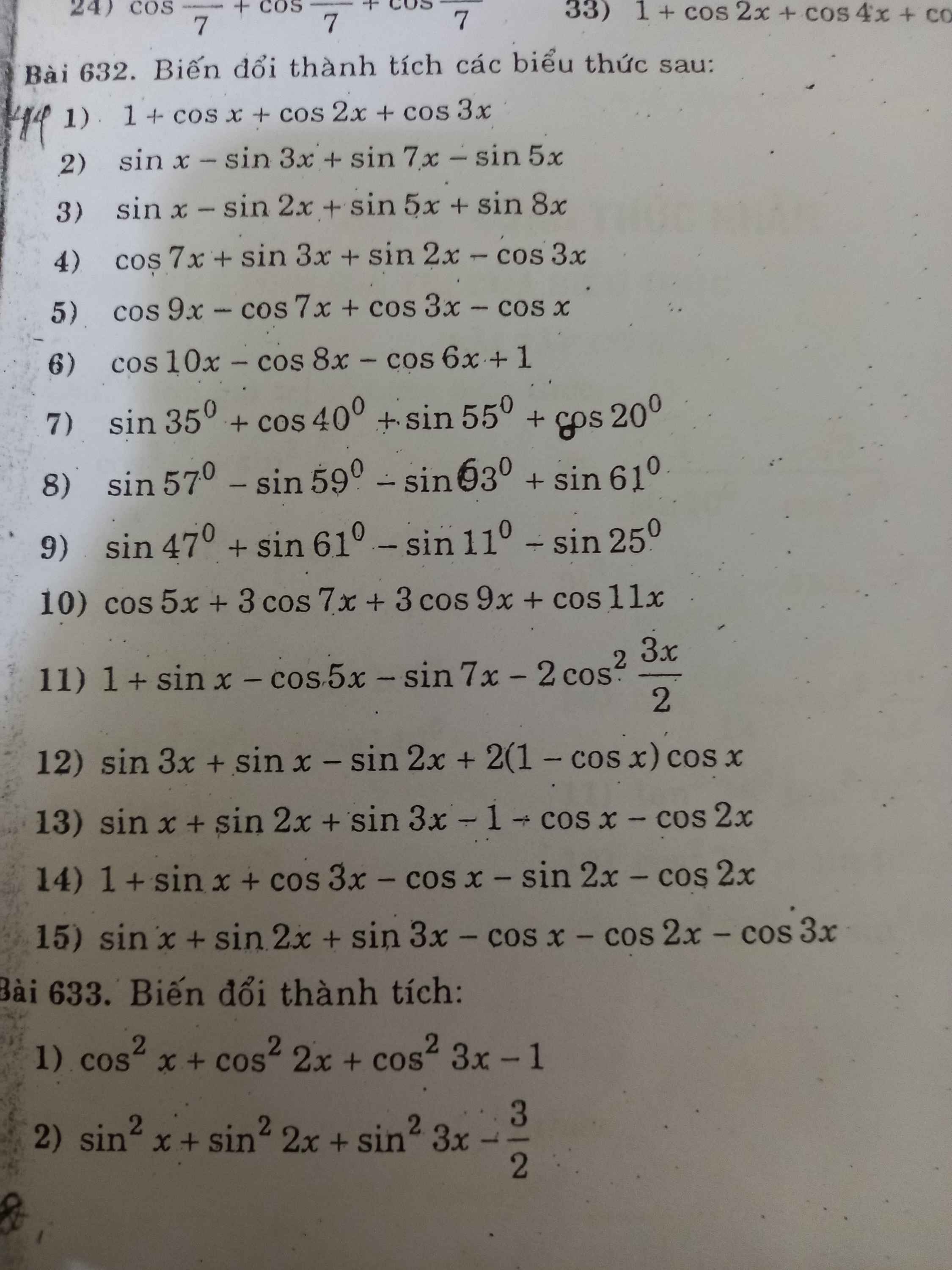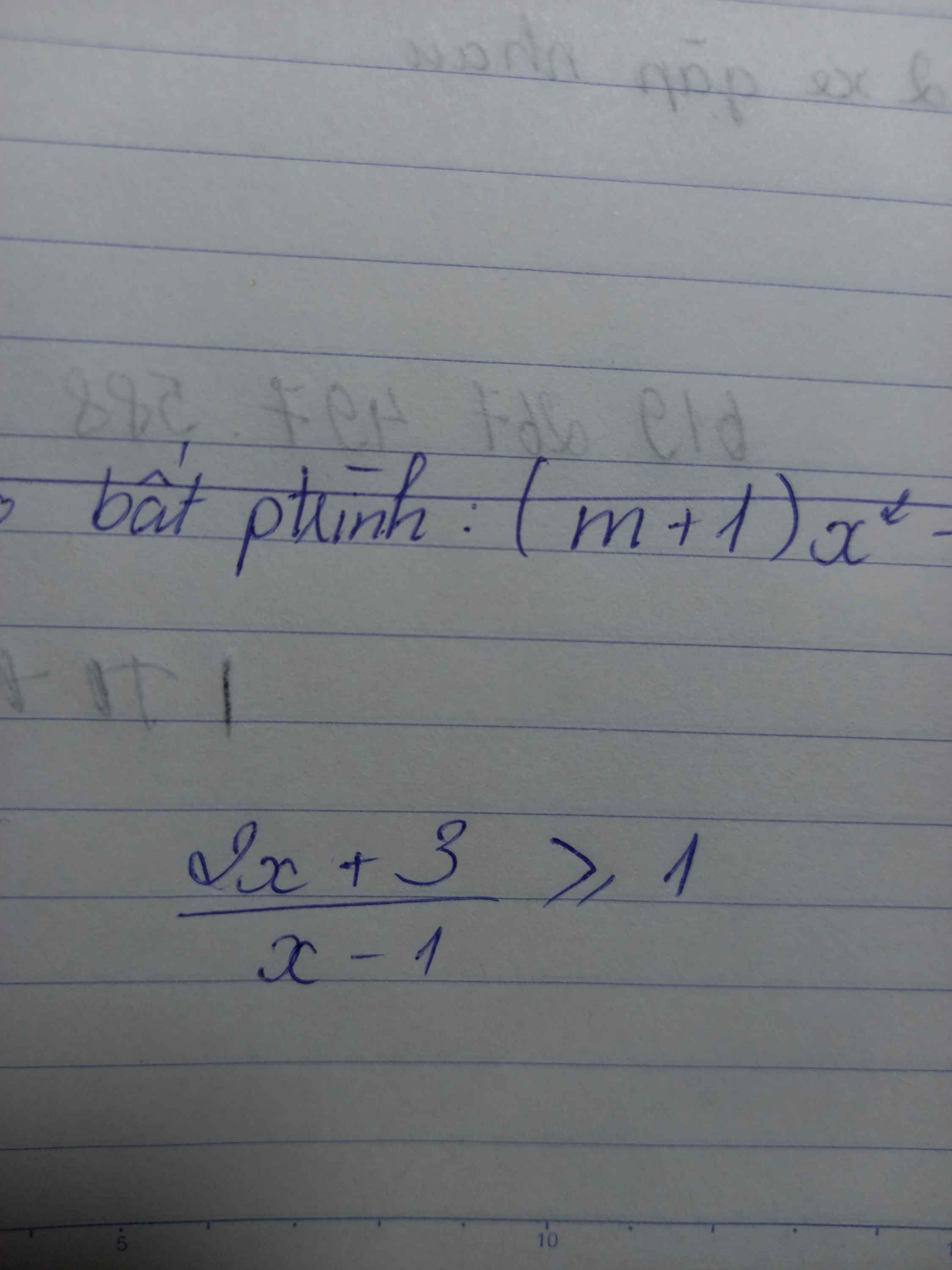\(x\in\left(\pi;\dfrac{3\pi}{2}\right)\Rightarrow\cos x< 0\)
Theo đề: \(\sin x=-\dfrac{7}{8}\Rightarrow\cos x=-\sqrt{1-\sin^2x}=-\dfrac{\sqrt{15}}{8}\)
\(\Rightarrow\tan x=\dfrac{\sin x}{\cos x}=\dfrac{7\sqrt{15}}{15}\)
Thay vào biểu thức P, tính được: \(P=\dfrac{\dfrac{7\sqrt{15}}{15}}{\left(\dfrac{7\sqrt{15}}{15}\right)^2+3}=\dfrac{7\sqrt{15}}{94}\)
Vậy khẳng định d là sai
\(cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{15}}{8}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{7}{\sqrt{15}}\)
\(\Rightarrow P=\dfrac{tanx}{tan^2x+3}=\dfrac{7\sqrt{15}}{94}\)
Nên khẳng định d sai
Thực chất ko cần tính ta cũng biết nó sai, vì trên \(\left(\pi;\dfrac{3\pi}{2}\right)\) thì \(tanx>0\) nên chắc chắn \(\dfrac{tanx}{tan^2x+3}>0\)
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
