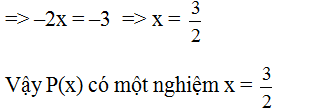a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.
muốn P(x) có nghiệm thì
P(x) = 3 - 2x = 0
= 2x = 3
x= 3 :2
x = 1,5
Q(x) = x^2+2 vì
x^2 luôn luôn > hoặc = 0
x^2 + 2 > 0
Vậy x^2+x vô nghiệm
a)
Cho đa thức P(x) = 0
=> 3 - 2x = 0
2x = 3 - 0
2x = 3
x = 3 : 2
x = \(\dfrac{3}{2}\)
Vậy đa thức P(x) có nghiệm là \(\dfrac{3}{2}\)
b)
Cho đa thức Q(x) = 0
=> \(x^2\) + 2 = 0
Mà \(x^2\) > hoặc = 0 ( với mọi x )
Nên \(x^2\) + 2 > 0 ( với mọi x )
=> \(x^2\) + 2 = 0 ( vô lí )
Vậy đa thức Q(x) không có nghiệm
x2 ≥ 0 ∀x ∈ R.
2 > 0
=> Q(x) = x2 + 2 > 0 ∀x ∈ R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.
(Lưu ý: với mọi giá trị x bất kì thì giá trị của biểu thức có số mũ chẵn (ví dụ: x2, x4, ...) thì đều luôn lớn hơn hoặc bằng 0.
Hay nói cách khác: nhân 2, 4, ... số nguyên cùng dấu (ví dụ: x2 = x.x) thì luôn có giá trị lớn hơn hoặc bẳng 0.)