bn nhan linh tinh ak? s ko cko so dai ho nua, ngan wa troi lun ak
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
So sánh:
x=\(\sqrt{6+\sqrt{6+...+\sqrt{6}}}+\sqrt{30+\sqrt{30+...+\sqrt{30}}}\)và y=\(\sqrt{89}\)
CMR \(\frac{1}{2}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+...+\frac{1}{2010\sqrt{2009}}< \frac{89}{45}\)
Chứng minh rằng \(\frac{87}{89}<\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+....+\frac{1}{2011\sqrt{2010}}<\frac{88}{45}\)
Ai biết gì giúp mình bài này hơi khó chút
Cộng các căn sau;sqrt{12}+sqrt{120}sqrt{2010}+sqrt{2022}sqrt{25+68}+sqrt{25+85}sqrt{25+26}+sqrt{25}sqrt{25+66+89}sqrt{25+69+55}+sqrt{58}+sqrt{59}sqrt{258+66}sqrt{2015+2013}
Đọc tiếp
Cộng các căn sau;
\(\sqrt{12}+\sqrt{120}\)
\(\sqrt{2010}+\sqrt{2022}\)
\(\sqrt{25+68}+\sqrt{25+85}\)
\(\sqrt{25+26}+\sqrt{25}\)
\(\sqrt{25+66+89}\)
\(\sqrt{25+69+55}+\sqrt{58}+\sqrt{59}\)
\(\sqrt{258+66}\)
\(\sqrt{2015+2013}\)
Cho 2015 số nguyên dương a1,a2,a3,...a2015 thỏa mãn điều kiện \(\frac{1}{\sqrt{a_1}}\) + \(\frac{1}{\sqrt{a_2}}\) + \(\frac{1}{\sqrt{a_3}}\) + ...+ \(\frac{1}{\sqrt{a_{2015}}}\) lớn hơn hoặc bằng 89. CMR: trong 2015 số nguyên dương đó, luôn tồn tại ít nhất 2 số bằng nhau.
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.
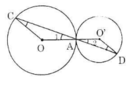
Hình 89
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.
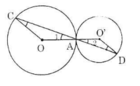
Hình 89
Tính:
(sin 1 độ + sin 2 độ + ... + sin 89 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)
TÌM X BIẾT :
X+5=123
X-45=89
X54-89+45=12457986
X chỉ là một số duy nhất












