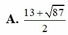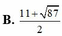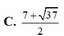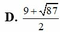Đặt \(\left(\dfrac{x}{4};\dfrac{y}{2};z\right)=\left(a;b;c\right)\Rightarrow a;b;c\ge0\)
Theo giả thiết: \(16^a+16^b+16^c=34\)
Đồng thời do \(a;b;c\ge0\Rightarrow\left\{{}\begin{matrix}16^a\ge1\\16^b\ge1\end{matrix}\right.\)
\(\Rightarrow\left(16^a-1\right)\left(16^b-1\right)\ge0\)
\(\Rightarrow16^{a+b}+1\ge16^a+16^b\) (1)
Lại có \(a+b\ge0\Rightarrow16^{a+b}\ge1\)
\(\Rightarrow\left(16^{a+b}-1\right)\left(16^c-1\right)\ge0\)
\(\Rightarrow16^{a+b+c}+1\ge16^{a+b}+16^c\) (2)
Cộng vế (1) và (2)
\(\Rightarrow16^{a+b+c}+2\ge16^a+16^b+16^c=34\)
\(\Rightarrow16^{a+b+c}\ge32\)
\(\Rightarrow a+b+c\ge log_{16}32=\dfrac{5}{4}\)
\(\Rightarrow P_{min}=\dfrac{5}{4}\)