để 20\(⋮2n+1\)
=> \(\dfrac{20}{2n+1}\) phải nguyên thì
2n+1\(\inƯ\left(20\right)=\left\{\pm1;\pm2;\pm4;\pm5;\pm10;\pm20\right\}\)
ta có bảng sau
| 2n+1 | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| 2n | -21 | -11 | -6 | -5 | -3 | -2 | 0 | 1 | 3 | 4 | 9 | 19 |
| n | \(-\dfrac{21}{2}\) | \(-\dfrac{11}{2}\) | -3 | -\(\dfrac{5}{2}\) | -\(\dfrac{3}{2}\) | -1 | 0 | \(\dfrac{1}{2}\) | \(\dfrac{3}{2}\) | 2 | \(\dfrac{9}{2}\) | \(\dfrac{19}{2}\) |
vậy .....











 Ai làm được mik tích cho, hạn là ngày hôm nay (Cứu!!!!!!)
Ai làm được mik tích cho, hạn là ngày hôm nay (Cứu!!!!!!)
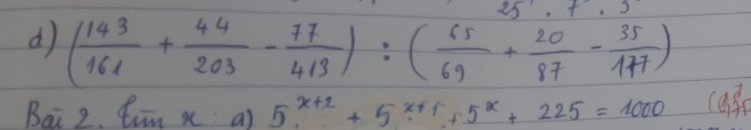 giúp mik với mik học kém quá
giúp mik với mik học kém quá