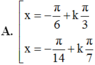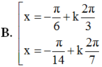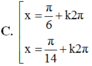\(2\cdot sin\left(x-\dfrac{\Omega}{3}\right)=1\)
=>\(sin\left(x-\dfrac{\Omega}{3}\right)=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x-\dfrac{\Omega}{3}=\dfrac{\Omega}{6}+k2\Omega\\x-\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{6}+k2\Omega=\dfrac{5}{6}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{6}+\dfrac{\Omega}{3}+k2\Omega=\dfrac{\Omega}{2}+k2\Omega\\x=\dfrac{5}{6}\Omega+\dfrac{\Omega}{3}+k2\Omega=\dfrac{7}{6}\Omega+k2\Omega\end{matrix}\right.\)
\(-\Omega< x< \Omega\)
=>\(\left[{}\begin{matrix}-\Omega< \dfrac{\Omega}{2}+k2\Omega< \Omega\\-\Omega< \dfrac{7}{6}\Omega+k2\Omega< \Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-1< \dfrac{1}{2}+2k< 1\\-1< \dfrac{7}{6}+2k< 1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}-\dfrac{3}{2}< 2k< \dfrac{1}{2}\\-\dfrac{13}{6}< 2k< -\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-\dfrac{3}{4}< k< \dfrac{1}{4}\\-\dfrac{13}{12}< k< -\dfrac{1}{12}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{6}+k2\Omega=\dfrac{\Omega}{6}+0\cdot2\Omega=\dfrac{\Omega}{6}\\x=\dfrac{7}{6}\Omega+\left(-1\right)\cdot2\Omega=-\dfrac{5}{6}\Omega\end{matrix}\right.\)