a) \(x=3\) là nghiệm của Pt cho ta có :
\(3^2+3\left(m+2\right)+2m=0\)
\(\Leftrightarrow5m=-15\)
\(\Leftrightarrow m=-3\)
Thay \(m=-3\) vào Pt cho ta được :
\(x^2-x-6=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\) có 1 nghiệm \(x=3\)
\(\Rightarrow x=-2\) là nghiệm còn lại
b) Áp dụng định lý Viète \(\left\{{}\begin{matrix}x_1+x_2=-\left(m+2\right)\left(1\right)\\x_1x_2=2m\left(2\right)\end{matrix}\right.\)
Phương trình cho có \(2\) nghiệm phân biệt \(x_1;x_2\) khi và chỉ khi
\(\Leftrightarrow\Delta=\left(m+2\right)^2-4m>0\Leftrightarrow m^2+4>0\left(đúng;\forall m\in R\right)\)
Theo đề bài ta có :
\(2x_1+3x_2=1\)
\(\Leftrightarrow2\left(x_1+x_2\right)+x_2=1\)
\(\Leftrightarrow x_2=1+2\left(m+2\right)=2m+5\)
\(\left(1\right)\Rightarrow x_1=-m-2-2m-5=-3m-7\)
\(\left(2\right)\Rightarrow\left(-3m-7\right)\left(2m+5\right)=2m\)
\(\Leftrightarrow-6m^2-29m-35=2m\)
\(\Leftrightarrow6m^2+31m+35=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{5}{3}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy với \(\left[{}\begin{matrix}m=-\dfrac{5}{3}\\m=-\dfrac{7}{2}\end{matrix}\right.\) thỏa mãn đề bài






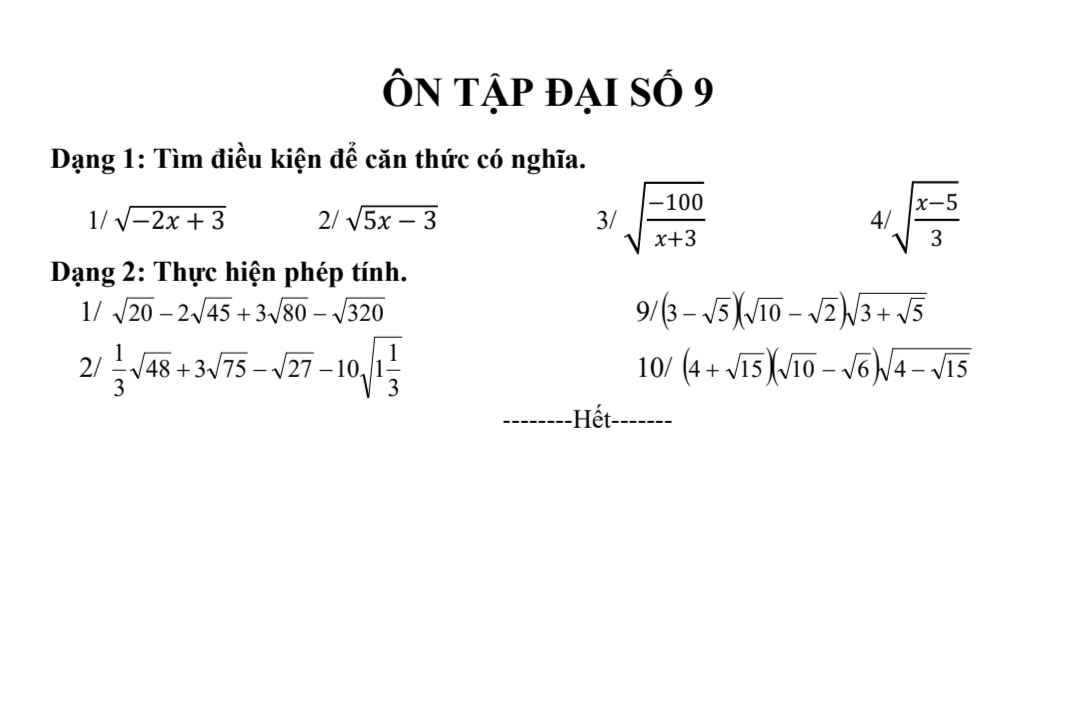


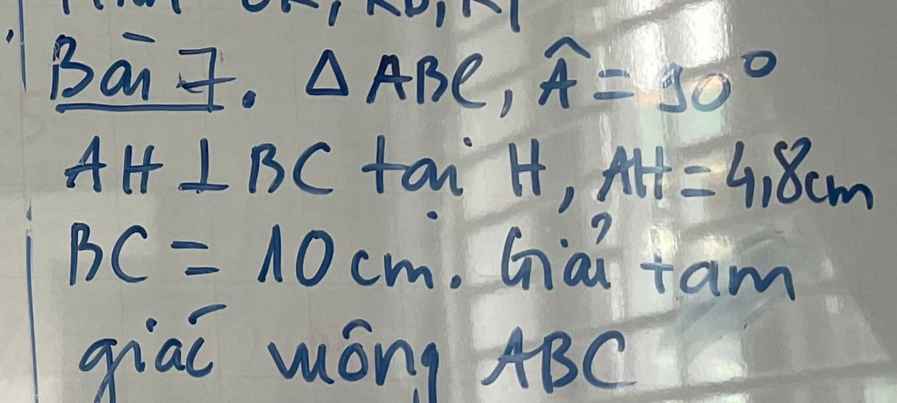









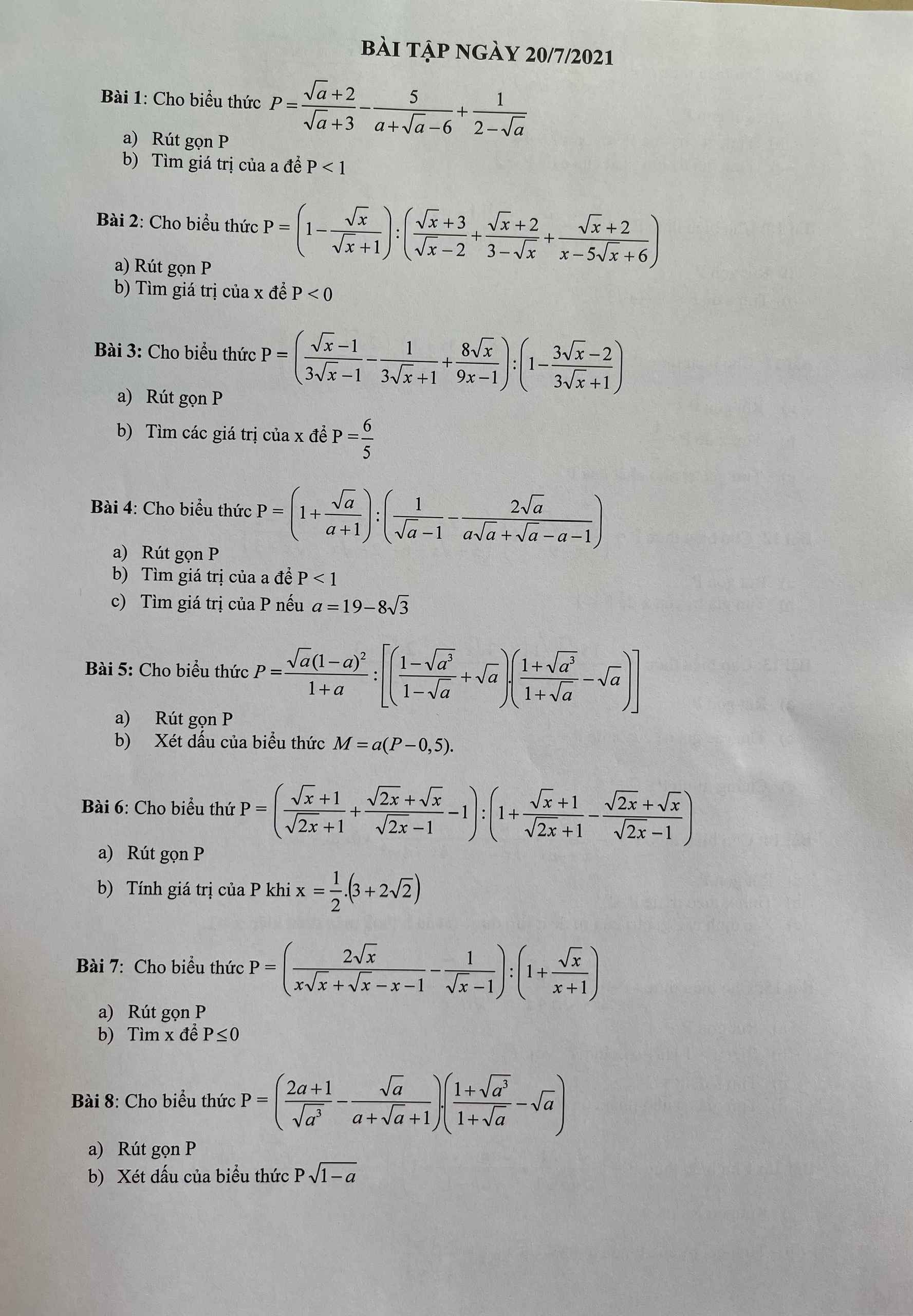 Gíup em với em đang cần gấp ạ^^
Gíup em với em đang cần gấp ạ^^
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
