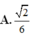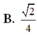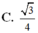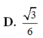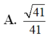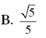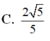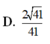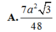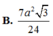1.Cho tứ diện đều ABCD . Gọi M , N , P lần lượt là trung điểm của Ab , CB , AD và G là trọng tâm tam giác , tính cos giữa 2 vecto MG và NP
2.Cho hình hộp ABCD.A'B'C'D' . Một đường thẳng \(\Delta\) cắt đường thẳng AA' , BC , C'D' lần lượt tại M,N,P sao cho \(\overrightarrow{NM}=2\overrightarrow{NP}\) . Tính tỉ số \(\dfrac{MA}{MA'}\)

1. G là trọng tâm tam giác nào em?
2.
Trong mp (ABCD), gọi Q là giao điểm AN và CD \(\Rightarrow Q\in\left(AMN\right)\)
3 mặt phẳng (AMN), (ADD'A'), (DCC'D') cắt nhau theo 3 giao tuyến phân biệt là AM, PQ, DD' nên 3 giao tuyến này song song hoặc đồng quy
Mà \(AM||DD'\) (do M thuộc AA') \(\Rightarrow AM||PQ||DD'\) (1)
\(\overrightarrow{NM}=2\overrightarrow{NP}\Rightarrow P\) là trung điểm NM (2)
(1);(2) \(\Rightarrow PQ\) là đường trung bình tam giác AMN
\(\Rightarrow PQ=\dfrac{1}{2}AM\) mà \(PQ=DD'=AA'\Rightarrow AM=2AA'\)
\(\Rightarrow\dfrac{MA}{MA'}=2\)
Câu 21 hàm S người ta thiết lập được như sau:

Theo đề bài thì \(AC=AB=BD=10\)
Kẻ AE và BF vuông góc CD
\(\Rightarrow AE=BF=AC.sin\phi=10sin\phi\)
\(CE=DF=AC.cos\phi=10cos\phi\)
\(\Rightarrow CD=CE+EF+DF=2.10cos\phi+10=20cos\phi+10\)
\(\Rightarrow S=\dfrac{\left(AB+CD\right).AE}{2}=\dfrac{\left(20cos\phi+10+10\right).10sin\phi}{2}=100sin\phi\left(cos\phi+1\right)\)
\(S'=100cos\phi\left(cos\phi+1\right)-100sin\phi.sin\phi\)
\(=100cos\phi\left(cos\phi+1\right)-100sin^2\phi=100cos\phi\left(cos\phi+1\right)-100\left(1-cos^2\phi\right)\)
\(=100cos\phi\left(cos\phi+1\right)-100\left(1-cos\phi\right)\left(1+cos\phi\right)\)
\(=100.\left(1+cos\phi\right)\left[2cos\phi-1\right]\)
\(S'=0\Rightarrow\left[{}\begin{matrix}cos\phi=-1\left(loại\right)\\cos\phi=\dfrac{1}{2}\end{matrix}\right.\) (loại do \(0\le\phi\le\dfrac{\pi}{2}\Rightarrow cos\phi\ge0\))
\(\Rightarrow sin\phi=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow S=100.\dfrac{\sqrt{3}}{2}\left(\dfrac{1}{2}+1\right)=75\sqrt{3}\)
À quên người ta hỏi góc \(\phi=\dfrac{\pi}{3}\)
1.
Đặt độ dài cạnh tứ diện là a
Qua G kẻ đường thẳng song song NP cắt AD tại E
\(\Rightarrow\) Góc giữa \(\overrightarrow{MG}\) và \(\overrightarrow{NP}\) bằng góc giữa \(\overrightarrow{MG}\) và \(\overrightarrow{GE}\)
\(\Rightarrow cos\left(\overrightarrow{MG};\overrightarrow{NP}\right)=-cos\left(\overrightarrow{GM};\overrightarrow{GE}\right)=-cos\widehat{MGE}\)
\(AN=ND\) (trung tuyến 2 tam giác bằng nhau) \(\Rightarrow\Delta AND\) cân tại N
\(\Rightarrow NP\perp AD\)
\(NP=\sqrt{ND^2-DP^2}=\sqrt{\left(\dfrac{a\sqrt{3}}{2}\right)^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
Talet: \(\dfrac{GE}{NP}=\dfrac{DG}{DN}=\dfrac{2}{3}\Rightarrow GE=\dfrac{2}{3}NP=\dfrac{a\sqrt{2}}{3}\)
G là trọng tâm BCD \(\Rightarrow AG\perp\left(BCD\right)\Rightarrow\Delta ABG\) vuông tại G
\(\Rightarrow GM=\dfrac{1}{2}AB=\dfrac{a}{2}\) (trung tuyến ứng với cạnh huyền)
\(AE=AD-DE=a+\dfrac{2}{3}.\left(\dfrac{a}{2}\right)=\dfrac{2a}{3}\)
Định lý hàm cos:
\(ME=\sqrt{AM^2+AE^2-2AM.AE.cos60^0}=\dfrac{\sqrt{13}}{6}\)
\(\Rightarrow cos\left(\overrightarrow{MG};\overrightarrow{NP}\right)=-cos\widehat{MGE}=-\dfrac{MG^2+GE^2-ME^2}{2MG.GE}=-\dfrac{\sqrt{2}}{6}\)