\(\dfrac{1+3\sqrt{2}-2\sqrt{3}}{\sqrt{6}+\sqrt{3}+\sqrt{2}}=\dfrac{1+3\sqrt{2}-2\sqrt{3}}{\sqrt{6}+\left(\sqrt{3}+\sqrt{2}\right)}\)
\(=\dfrac{\left(1+\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)\right)\left(\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right)}{\left(\sqrt{6}+\left(\sqrt{3}+\sqrt{2}\right)\right)\left(\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right)}\)
\(=\dfrac{\left(\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right)+\left(\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)\right)\left(\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right)}{6-\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\dfrac{\left(\sqrt{6}-\left(\sqrt{3}+\sqrt{2}\right)\right)+6\left(\sqrt{3}-\sqrt{2}\right)-\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}{6-\left(3+2+2\sqrt{6}\right)}\)
\(=\dfrac{\sqrt{6}-\sqrt{3}-\sqrt{2}+6\sqrt{3}-6\sqrt{2}-\sqrt{6}}{6-5-2\sqrt{6}}\)
\(=\dfrac{5\sqrt{3}-8\sqrt{2}}{1-2\sqrt{6}}\)
\(=\sqrt{3}-\sqrt{2}\)
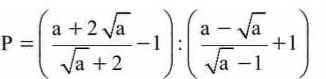Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)
