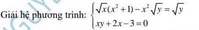\(\left\{{}\begin{matrix}\sqrt{x}\left(x^2+1\right)-x^2\sqrt{y}=\sqrt{y}\left(1\right)\\xy+2x-3=0\left(2\right)\end{matrix}\right.\left(x,y\ge0\right)\)
\(\left(1\right)\Leftrightarrow x^2\sqrt{x}-x^2\sqrt{y}+\sqrt{x}-\sqrt{y}=0\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\Rightarrow\sqrt{x}=\sqrt{y}\Rightarrow x=y\)
Thế vào (2) \(\Rightarrow x^2+2x-3=0\Rightarrow\left(x-1\right)\left(x+3\right)=0\)
mà \(x\ge0\Rightarrow x=1\Rightarrow x=y=1\)
Đúng 0
Bình luận (0)
