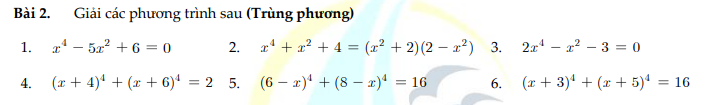Question

Bài 2. Giải các phương trình sau (Trùng phương)

1. \(x^4 - 5x^2 + 6 = 0\)

2. \(x^4 + x^2 + 4 = (x^2 + 2)(2 - x^2)\)

3. \(2x^4 - x^2 - 3 = 0\)

4. \((x + 4)^4 + (x + 6)^4 = 2\)

5. \((6 - x)^4 + (8 - x)^4 = 16\)

6. \((x + 3)^4 + (x + 5)^4 = 16\)

Answer 1

1: \(x^4-5x^2+6=0\)

=>\(x^4-2x^2-3x^2+6=0\)

=>\(\left(x^2-2\right)\left(x^2-3\right)=0\)

=>\(\left[{}\begin{matrix}x^2-3=0\\x^2-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2=3\\x^2=2\end{matrix}\right.\Leftrightarrow x\in\left\{\sqrt{3};-\sqrt{3};-\sqrt{2};\sqrt{2}\right\}\)

2: \(x^4+x^2+4=\left(x^2+2\right)\left(2-x^2\right)\)

=>\(x^4+x^2+4=4-x^4\)

=>\(2x^4+x^2=0\)

=>\(x^2\left(2x^2+1\right)=0\)

mà \(2x^2+1>=1>0\forall x\)

nên \(x^2=0\)

=>x=0

3: \(2x^4-x^2-3=0\)

=>\(2x^4-3x^2+2x^2-3=0\)

=>\(\left(2x^2-3\right)\left(x^2+1\right)=0\)

mà \(x^2+1>=1>0\forall x\)

nên \(2x^2-3=0\)

=>\(x^2=\dfrac{3}{2}\)

=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{2}\\x=-\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)

4: \(\left(x+4\right)^4+\left(x+6\right)^4=2\) 

Đặt x+5=a

=>a-1=x+4; a+1=x+6

Phương trình sẽ trở thành:

\(\left(a-1\right)^4+\left(a+1\right)^4=2\)

=>\(a^4-4a^3+6a^2-4a+1+a^4+4a^3+6a^2+4a+1-2=0\)

=>\(2a^4+12a^2=0\)

=>\(2a^2\left(a^2+6\right)=0\)

=>\(a^2=0\)

=>a=0

=>x+5=0

=>x=-5

5: \(\left(6-x\right)^4+\left(8-x\right)^4=16\)

=>\(\left(x-6\right)^4+\left(x-8\right)^4=16\)

Đặt a=x-7

=>a+1=x-6; a-1=x-8

Phương trình sẽ trở thành:

\(\left(a+1\right)^4+\left(a-1\right)^4=16\)

=>

=>\(a^4-4a^3+6a^2-4a+1+a^4+4a^3+6a^2+4a+1=16\)

=>\(2a^4+12a^2+2-16=0\)

=>\(2a^4+12a^2-14=0\)

=>\(a^4+6a^2-7=0\)

=>\(\left(a^2+7\right)\left(a^2-1\right)=0\)

mà \(a^2+7>=7>0\forall a\)

nên \(a^2-1=0\)

=>\(a^2=1\)

=>\(\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-7=1\\x-7=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=6\end{matrix}\right.\)

6: \(\left(x+3\right)^4+\left(x+5\right)^4=16\)

Đặt x+4=a

=>x+3=a-1; x+5=a+1

Phương trình sẽ trở thành:

\(\left(a-1\right)^4+\left(a+1\right)^4=16\)

=>\(a^4-4a^3+6a^2-4a+1+a^4+4a^3+6a^2+4a+1=16\)

=>\(2a^4+12a^2+2-16=0\)

=>\(2a^4+12a^2-14=0\)

=>\(a^4+6a^2-7=0\)

=>\(\left(a^2+7\right)\left(a^2-1\right)=0\)

mà \(a^2+7>=7>0\forall a\)

nên \(a^2-1=0\)

=>\(a^2=1\)

=>\(\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+4=1\\x+4=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)