Đặt \(g\left(x\right)=f\left(x^2+1\right)\Rightarrow g'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=1\\x^2+1=3\\x^2+1=4\end{matrix}\right.\) \(\Rightarrow x=\left\{0;\pm\sqrt{2};\pm\sqrt{3}\right\}\)
BBT g(x):
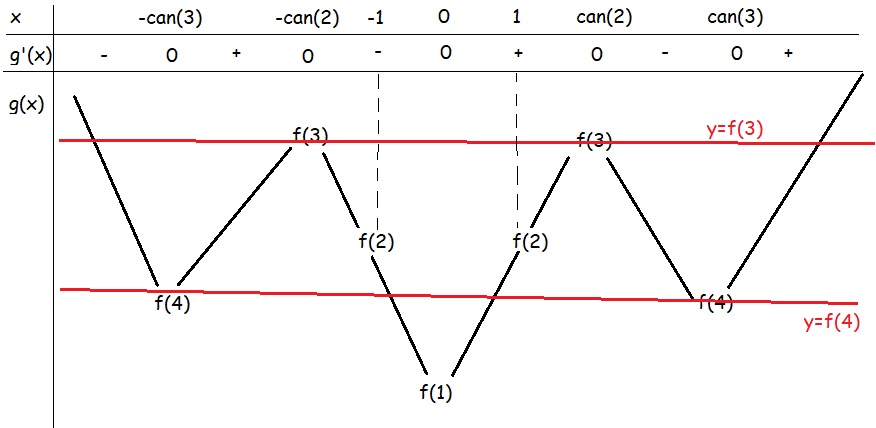
Nên:
c.
\(f\left(x^2+1\right)=f\left(3\right)\) có 4 nghiệm (trong đó có 2 nghiệm kép)
d.
\(f\left(1\right)+f\left(3\right)=f\left(2\right)+f\left(4\right)\Rightarrow f\left(4\right)-f\left(1\right)=f\left(3\right)-f\left(2\right)>0\)
\(\Rightarrow f\left(4\right)>f\left(1\right)\)
Nên BBT có dạng như trên nên \(f\left(x^2+1\right)=f\left(4\right)\) có 4 nghiệm (2 nghiệm đơn và 2 nghiêmk kép)










