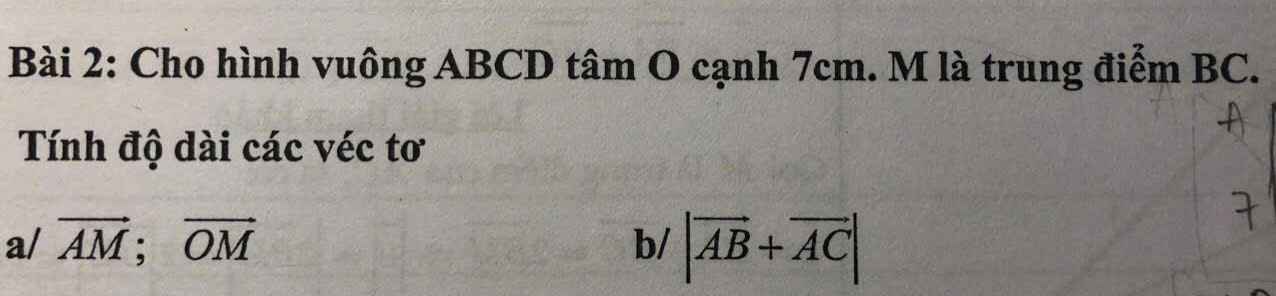a:
ABCD là hình vuông có tâm O
=>O là trung điểm của AC
Xét ΔCAB có
O,M lần lượt là trung điểm của CA,CB
=>OM là đường trung bình của ΔCAB
=>OM//AB và \(OM=\dfrac{1}{2}AB=3,5\left(cm\right)\)
\(\left|\overrightarrow{OM}\right|=OM=3,5\left(cm\right)\)
ΔABM vuông tại B
=>\(BA^2+BM^2=AM^2\)
=>\(AM=\sqrt{7^2+\left(3,5\right)^2}=\dfrac{7\sqrt{5}}{2}\)
=>\(\left|\overrightarrow{AM}\right|=AM=\dfrac{7\sqrt{5}}{2}\left(cm\right)\)
b: Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
M là trung điểm của BC
=>\(BM=\dfrac{BC}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AM}\right|=2\cdot AM=2\cdot\dfrac{7\sqrt{5}}{2}=7\sqrt{5}\left(cm\right)\)