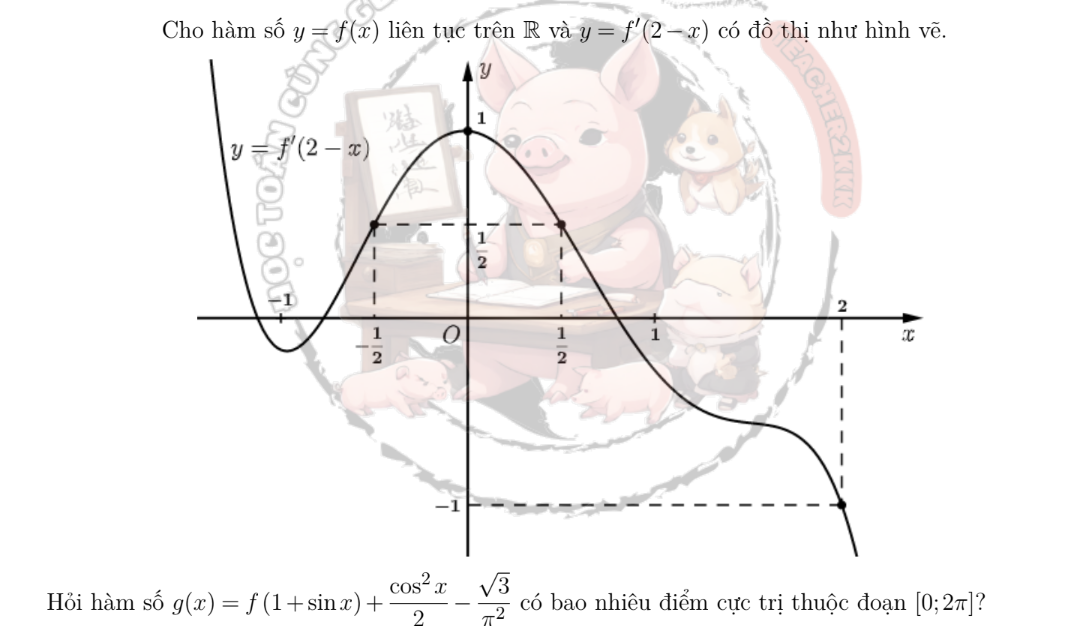
\(g'=cosx.f'\left(1+sinx\right)-sinx.cosx=0\Rightarrow\left[{}\begin{matrix}cosx=0\\f'\left(1+sinx\right)=sinx\end{matrix}\right.\)
\(1+sinx=2-t\Rightarrow sinx=1-t\) với \(0\le t\le2\)
\(\Rightarrow f'\left(2-t\right)=1-t\)
Đường \(y=1-t\) cắt \(f'\left(2-t\right)\) tại 4 điểm \(t=0,\dfrac{1}{2};a;2\) trên [0;2]
\(\Rightarrow sinx=1;\dfrac{1}{2};1-a;-1\)
\(sinx=1\) và \(sinx=-1\) cho nghiệm kép (loại)
Còn lại \(sinx=\dfrac{1}{2};1-a\) cho 4 nghiệm
Cosx=0 cho 2 nghiệm
\(\Rightarrow6\) cực trị
Đúng 3
Bình luận (0)
