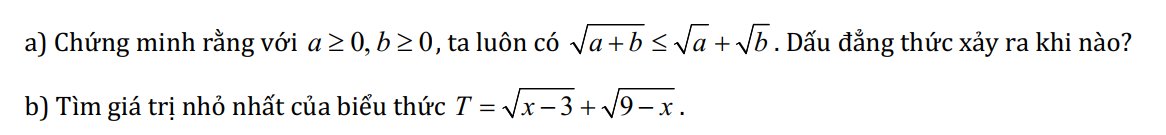a) \(\sqrt{a+b}\le\sqrt{a}+\sqrt{b}\)
\(\Leftrightarrow\left(\sqrt{a+b}\right)^2\le\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\Leftrightarrow a+b\le a+b+2\sqrt{ab}\)
\(\Leftrightarrow2\sqrt{ab}\ge0\)
\(\Leftrightarrow ab\ge0\left(luôn.đúng\right)\)
Vậy \(\sqrt{a+b}\le\sqrt{a}+\sqrt{b}\) \(\left(a;b\ge0\right)\)
Dấu "=" xảy ra khi và chỉ khi \(\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\)
b) Sửa đề bài tìm GTLN
\(T=\sqrt{x-3}+\sqrt{9-x}\)
Áp dụng bất đẳng thức Bunhiacopxki ta có :
\(T^2=\left(\sqrt{x-3}+\sqrt{9-x}\right)^2\le2.\left(x-3+9-x\right)=12\)
\(\Rightarrow T\le2\sqrt{3}\)
\(\Rightarrow GTLN\left(T\right)=2\sqrt{3}\) tại \(x=6\)