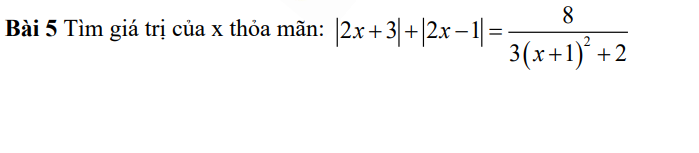\(\left|2x+3\right|+\left|2x-1\right|=\dfrac{8}{3\left(x+1\right)^2+1}\)
Ta có :
\(\left|2x+3\right|+\left|2x-1\right|\ge\left|2x+3+2x-1\right|=\left|4x+2\right|\left(1\right)\)
Dấu '=' xảy ra khi và chỉ khi
\(\left(2x+3\right)\left(2x-1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{3}{2}\\x\ge\dfrac{1}{2}\end{matrix}\right.\)
Ta lại có :
\(3\left(x+1\right)^2\ge0,\forall x\in R\)
\(\Rightarrow3\left(x+1\right)^2+2\ge2\)
\(\Rightarrow\dfrac{1}{3\left(x+1\right)^2+2}\le\dfrac{1}{2}\)
\(\Rightarrow\dfrac{8}{3\left(x+1\right)^2+2}\le\dfrac{8}{2}=4\)
Dấu '=' xảy ra khi và chỉ khi \(x+1=0\Leftrightarrow x=-1\) thỏa \(\left(1\right)\)
Vậy \(x=-1\) thỏa đề bài