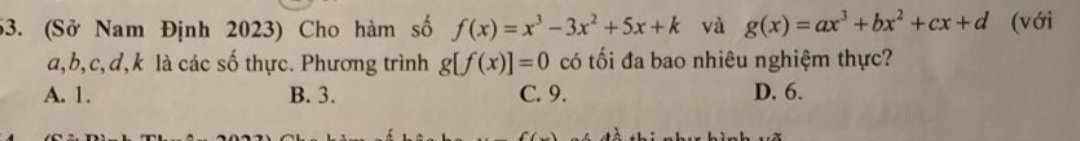\(f'\left(x\right)=3x^2-6x+5>0;\forall x\) \(\Rightarrow f\left(x\right)\) đồng biến trên R
\(y=g\left[f\left(x\right)\right]\Rightarrow y'=f'\left(x\right).g'\left[f\left(x\right)\right]\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\g'\left[f\left(x\right)\right]=0\end{matrix}\right.\)
\(f'\left(x\right)=0\) vô nghiệm theo cmt, \(g'\left[f\left(x\right)\right]\) có tối đa 2 nghiệm
\(\Rightarrow g\left[f\left(x\right)\right]\) có tối đa 2 cực trị nên \(g\left[f\left(x\right)\right]=0\) có tối đa 3 nghiệm
B đúng
Đúng 3
Bình luận (0)
