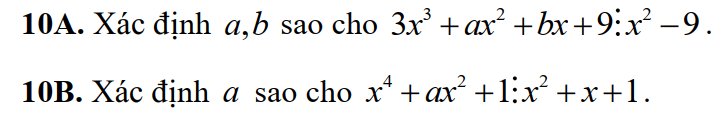10A
\(3x^3+ax^2+bx+9⋮x^2-9\left(1\right)\)
Để thỏa điều kiện (1) nên dạng của đa thức \(P=3x^3+ax^2+bx+9=\left(x^2-9\right)\left(cx+d\right)=cx^3+dx^2-9cx-9d\)
Điều kiện để đa thức P là các hệ số 2 vế bằng nhau.
\(\Rightarrow\left\{{}\begin{matrix}c=3\\d=a\\-9c=b\\-9d=9\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}c=3\\d=-1\\a=-1\\b=-27\end{matrix}\right.\)
Vậy \(\left(a;b\right)=\left(-1;27\right)\) thỏa mãn đề bài
10B.
\(x^4+ax^2+1⋮x^2+x+1\left(1\right)\)
Để thỏa điều kiện (1) nên dạng của đa thức
\(Q\left(x\right)=x^4+ax^2+1=\left(x^2+x+1\right)\left(cx^2+dx+e\right)\)
\(\Rightarrow Q\left(x\right)=cx^4+dx^3+ex^2+cx^3+dx^2+ex+cx^2+dx+e\)
\(\Rightarrow Q\left(x\right)=cx^4+\left(c+d\right)x^3+\left(c+d+e\right)x^2+\left(e+d\right)x+e\)
Điều kiện để đa thức Q(x) là các hệ số 2 vế bằng nhau.
\(c=1;c+d=0;c+d+e=a;c+d=0;e=1\)
\(\Rightarrow c=1;e=1;a=1;d=-1\)
Vậy \(a=1\) thỏa mãn đề bài