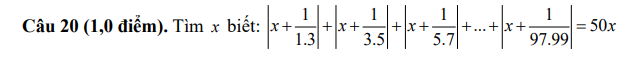Vì \(\left|x+\dfrac{1}{1.3}\right|\)+\(\left|x+\dfrac{1}{3.5}\right|\)+...+\(\left|x+\dfrac{1}{97.99}\right|\)=50x
mà\(\left|x+\dfrac{1}{1.3}\right|\)+\(\left|x+\dfrac{1}{3.5}\right|\)+...+\(\left|x+\dfrac{1}{97.99}\right|\) > 0(Vì các số hạng là các trị tuyệt đối)
⇒50x>0
⇒x>0
⇒\(\left|x+\dfrac{1}{1.3}\right|\)+\(\left|x+\dfrac{1}{3.5}\right|\)+...+\(\left|x+\dfrac{1}{97.99}\right|\) =x+\(\dfrac{1}{1.3}\)+x+\(\dfrac{1}{3.5}\)+...+x+\(\dfrac{1}{97.99}\)=49x+\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{97.99}\right)\)=50x
⇒49x+ \(\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)=50x
⇒1-\(\dfrac{1}{99}\)=50x-49x
⇒x=\(\dfrac{98}{99}\)
Vậy x=\(\dfrac{98}{99}\)