Question

Answer 1

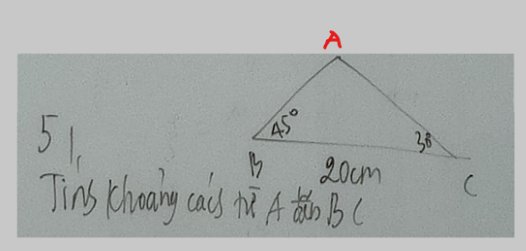
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(\widehat{A}=180^0-45^0-30^0=105^0\)

Xét ΔABC có \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)

=>\(\dfrac{AC}{sin45}=\dfrac{AB}{sin30}=\dfrac{20}{sin105}=20\sqrt{6}-20\sqrt{2}\)

=>\(AC=20\sqrt{3}-20\left(cm\right);AB=\dfrac{1}{2}\left(20\sqrt{6}-20\sqrt{2}\right)=10\sqrt{6}-10\sqrt{2}\left(cm\right)\)

\(S_{ACB}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB=\dfrac{1}{2}\cdot\left(20\sqrt{3}-20\right)\cdot20\cdot sin30\)

\(=5\left(20\sqrt{3}-20\right)=100\sqrt{3}-100\left(cm^2\right)\)

Khoảng cách từ A xuống BC là:

\(2\cdot\dfrac{S_{CAB}}{BC}=\dfrac{2\cdot\left(100\sqrt{3}-100\right)}{20}=2\left(5\sqrt{3}-5\right)=10\sqrt{3}-10\left(cm\right)\)