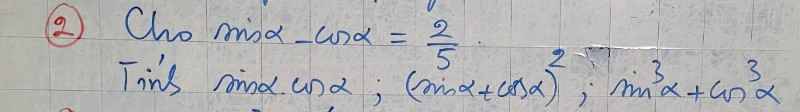a, \(\left(sina-cos\right)^2=\dfrac{4}{25}\Rightarrow sin^2a+cos^2a-2sinacosa=\dfrac{4}{25}\)
\(\Leftrightarrow2sinacosa=\dfrac{21}{25}\Leftrightarrow sinacosa=\dfrac{21}{50}\)
b, \(\left(sina+cosa\right)^2=sin^2a+2sinacosa+cos^2a=1+\dfrac{21}{25}=\dfrac{46}{25}\)
c, \(sin^3a+cos^3a=\left(sina+cos\right)\left(sin^2a-sinacosa+cos^2a\right)\)
Ta có \(\left(sina+cosa\right)^2=\dfrac{46}{25}\Leftrightarrow\left[{}\begin{matrix}sina+cosa=\dfrac{\sqrt{46}}{5}\\sina+cosa=-\dfrac{\sqrt{46}}{5}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}-1\le sina\le1\\-1\le cosa\le1\end{matrix}\right.\Rightarrow-2\le cosa+sina\le2\)
=> Lấy 2 th
TH1 : \(=\dfrac{\sqrt{46}}{5}\left(1-\dfrac{21}{50}\right)=\dfrac{29\sqrt{46}}{250}\)
TH2 : \(=-\dfrac{\sqrt{46}}{5}\left(1-\dfrac{21}{50}\right)=\dfrac{-29\sqrt{46}}{250}\)