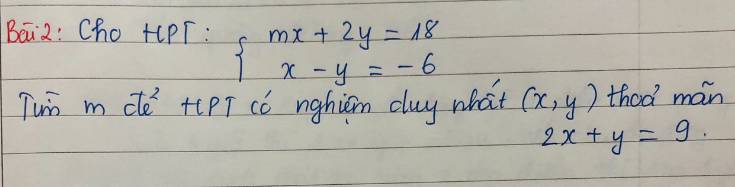Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{1}\ne\dfrac{2}{-1}=-2\)
=>\(m\ne-2\)
\(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}mx+2y=18\\2x-2y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(m+2\right)=6\\x-y=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{6}{m+2}\\y=x+6=\dfrac{6}{m+2}+6=\dfrac{6+6m+12}{m+2}=\dfrac{6m+18}{m+2}\end{matrix}\right.\)
2x+y=9
=>\(\dfrac{12}{m+2}+\dfrac{6m+18}{m+2}=9\)
=>\(\dfrac{6m+30}{m+2}=9\)
=>9(m+2)=6m+30
=>9m+18=6m+30
=>3m=12
=>m=4(nhận)
Đúng 3
Bình luận (0)
