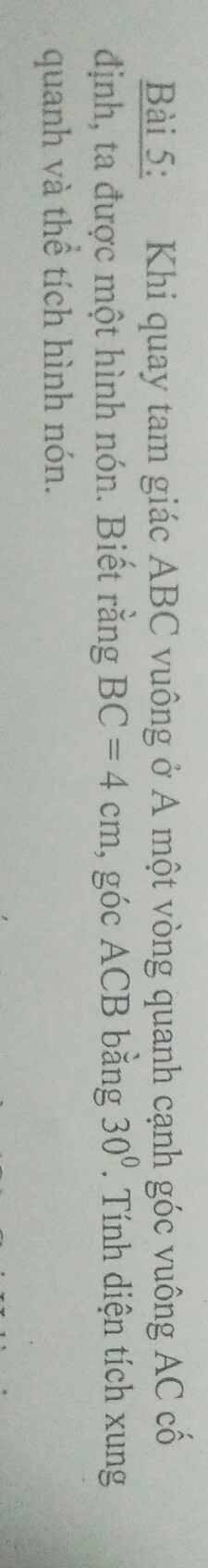Question

Answer 1

Trong tam giác vuông ABC:

\(AC=BC.cos\widehat{ACB}=4.cos30^0=2\sqrt{3}\left(cm\right)\)

\(AB=BC.sin\widehat{ACB}=4.sin30^0=2\left(cm\right)\)

Khi quay tam giác vuông quanh AC ta được 1 hình nón có chiều cao \(h=AC=2\sqrt{3}\left(cm\right)\), bán kính đáy \(R=AB=2\left(cm\right)\), độ dài đường sinh \(l=BC=4\left(cm\right)\)

Diện tích xung quanh nón là:

\(S_{xq}=\pi Rl=8\pi\left(cm^2\right)\)

Thể tích nón là:

\(V=\dfrac{1}{3}\pi R^2h=\dfrac{8\pi\sqrt{3}}{3}\left(cm^3\right)\)